The term group velocity defines the rate at which the envelope of a signal propagates in a transmission medium. This signal transmitted over the medium is obtained when a modulating signal modulates a central frequency, typically called the carrier [1]. As a result, the modulating signal and the envelope are equivalent. While the envelope propagates through the medium at the group velocity, the propagation velocity of the overall signal is called the phase velocity.
This article develops two different ways of proving the group velocity equation. It also displays moving graphs that allow to interpret the group velocity and to distinguish it from the phase velocity. The table of contents is as follows:
1. Brief History of Group Velocity
The concept of group velocity was originally enunciated by W. R. Hamilton. However, it was Lord Rayleigh who generalized the term and distinguished it from phase velocity. Sommerfeld later refined and modernized the earlier developments. Finally, Léon Brillouin, who was Sommerfeld’s pupil, continued his master’s efforts to clarify propagation in highly absorbing and dispersive media. His work [2] has become a modern reference for the study of group velocity in all types of media.
2. Phase Velocity vs. Group Velocity
This section discusses the difference between the propagation of a single frequency component and the case of a real signal composed of multiple tones.
2.1 Single-Tone Propagation
As a starting point it is considered the generic equation, f(x,t), of a single frequency component propagating at time t along the x-axis [2]:
\begin{equation} f(x,t) = \cos(\omega t - kx) \end{equation}
Where:
- \footnotesize \omega represents the angular frequency in rad/sg.
- \footnotesize k represents the propagation constant or wave number in rad/m.
The propagation velocity of the tone, called phase velocity \footnotesize v_p , can be easily derived by writing equation (1) as follows [2]:
\begin{equation} f(x,t) = \cos\left[\omega \left(t - \frac{x}{\omega / k}\right)\right] = \cos\left[\omega \left(t - \frac{x}{v_p}\right)\right] \end{equation}
\begin{equation} v_p = \frac{\omega}{k}\end{equation}
Note that \footnotesize k and \footnotesize \omega can be related by any function. Consequently the phase velocity can be frequency dependent.
2.2 Multi-Tone Propagation
Any signal carrying information is typically made up of a set of frequency components that are articulated around the carrier center frequency \footnotesize \omega_c [1]. Thus, it can be written a generic propagation equation composed of multiple components (of frequency \footnotesize \omega_i ) with their respective amplitudes (\footnotesize A_i ) and propagation constants (\footnotesize k_i ):
\begin{equation} f(x,t) = \sum_i A_i \cos(\omega_i t - k_ix) \end{equation}
\begin{equation} \omega_i = \omega_c + \Delta\omega_i \end{equation}
\begin{equation} k_i = k_c + \Delta k_i \end{equation}
Note that equation (4) should include a generic phase φi in all its frequency components, but it has not been added for simplicity and because it does not alter the conclusions of the text.
Given the complexity of the new frequency beat compared to the simple case of equation (1), the following questions arise. Can the modulating or envelope signal be easily separated from the carrier? And, more importantly, can the group velocity of the envelope and the velocity of the overall signal be distinguished? Both questions are answered below.
3. Group Velocity
In this section the group velocity is proved by two different techniques: in the time domain and in the frequency domain.
3.1 Time-Domain Proof
Simplifying equation (4), we start from a propagating signal s(x,t), composed of two tones of equal amplitude and with frequencies and propagation constants equidistant to the central frequency:
\begin{equation} s(x,t) = \frac{1}{2}\cos[(\omega_c - \Delta\omega) t - (k_{c}-\Delta k) x] + \frac{1}{2}\cos[(\omega_c + \Delta\omega) t - (k_{c}+\Delta k) x] \end{equation}
Applying the following trigonometric identities:
\begin{equation}\cos(a)+\cos(b) = 2\cos\left(\frac{a+b}{2}\right)\cos\left(\frac{a-b}{2}\right) \end{equation}
\begin{equation}\cos(\phi) = \cos(-\phi) \end{equation}
Equation (7) can be written as follows:
\begin{equation} s(x,t) = \underbrace{\cos(\Delta\omega t - \Delta k x)}_{\text{envelope}}·\underbrace{\cos(\omega_c t - k_{c}x)}_{\text{carrier}}\end{equation}
Since typically \footnotesize \Delta\omega << \omega_c , it is concluded that the signal can be expressed as a low-frequency envelope (\footnotesize \Delta\omega) modulated on a carrier (\footnotesize \omega_c ). This effect can be seen in Figure 1(a), which illustrates an example of s(x,\footnotesize t_o ), the x-axis representation of the signal for a particular generic instant \footnotesize t_o .
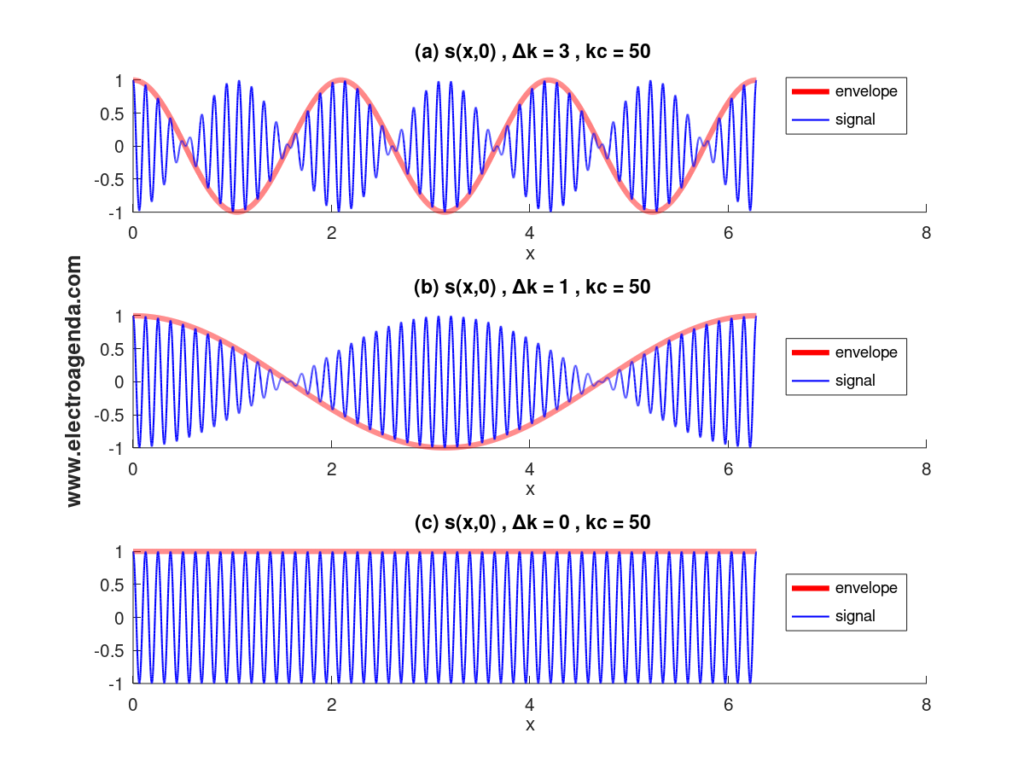
As follows, two cases can be distinguished. Firstly the particular case in which the group velocity is constant. Secondly the general case in which it varies with frequency.
3.1.1 Constant Group Velocity
From the demonstration to obtain equation (10) it is clear that a pair of frequency components can form a “group” or envelope propagating at a group velocity \footnotesize \Delta\omega/\Delta k . It should be noted that this definition is very restricted to a particular case, in line with equation (7). Specifically, it involves the propagation of two tones of equal amplitude and equidistantly separated from the carrier and its propagation constant (\footnotesize \Delta\omega y \footnotesize \Delta k ).
Under the same conditions and with the same constraints, if we consider a larger number of frequency components, each pair of tones around the carrier will give rise to another contribution to the envelope. And the propagation velocity of the group will be constant:
\begin{equation} v_{g_{constant}} = \frac{\Delta\omega}{\Delta k}\end{equation}
Furthermore, from equation (10) it also follows that the phase velocity of the whole signal is that of the carrier: \footnotesize v_p=\omega_c/k_c in line with equation (3). Therefore, if the function k(ω) of the medium is of the form k=a1ω (a1 being a constant), the velocities vp of the global signal and vg are constant and equal. On the other hand, if k=a1ω+a0 (a0 also being a constant), it follows that vp of the signal and vg are constant but different.
3.1.2 General Group Velocity
In practice, in a realistic situation, the propagating signal will not necessarily meet the conditions imposed in the previous section. First, a communications signal is composed of a spectral density with an arbitrary amplitude [1]. Moreover, in any given transmission medium, the propagation constant may vary non-uniformly with frequency.
Therefore, for a universal definition of the concept, differential calculus must be applied. The effect of reducing \footnotesize \Delta\omega and \footnotesize \Delta k to their respective differentials can be seen in Figure 1(c). Thus, it is shown that each frequency component of the signal has an associated group velocity given by:
\begin{equation} v_g = \frac{\partial\omega}{\partial k}\end{equation}
Although this definition is more general than the interpretation in section 3.1.1, the intrinsic complexity of the group velocity concept is still apparent. Indeed, when the it is constant in frequency, there is no doubt about the propagation velocity of the signal envelope. However, when the group velocity depends on frequency, the concept can become physically meaningless, since dispersion and signal distortion occur [2]. This point is more evident with the frequency domain demonstration, which is developed in the next section.
Finally, in our phase velocity analysis it is shown that an arbitrary sum of tones, as in equation (4), also allows to generalize the group velocity equation. However the phase velocity of the overall signal may not be equal to the phase velocity of the center frequency. This is because envelope and carrier cannot be separated with the simplicity shown in equation (10).
3.2 Frequency-Domain Proof
In this section the group velocity equation is demonstrated from the frequency domain. Previously it is recommended to review the Fourier transform in the domain of the propagation constant or wave number k, which is denoted F(k).
First, the calculations are simplified by using phasors instead of the tones used in equation (4). In this way the signal, which is composed of a real envelope e(x,t) and a carrier, is the result of integrating the phasors that compose it (equivalent to the inverse Fourier transform):
\begin{equation} \begin{split} f(x,t) &= e(x,t)\cos(k_cx - \omega_ct-\varphi(x,t)) \\ &= \frac{1}{2\pi} \int F(k)e^{j(kx-\omega t)}dk \end{split} \end{equation}
Where the term F(k) is the Fourier transform in the spatial domain for t=0:
\begin{equation} F(k) = \int f(x,0)e^{-jkx}dx\end{equation}
3.2.1 Narrow Band Group Velocity
Again, it is indicated that the frequency is related to the propagation constant by a function \footnotesize \omega(k) . Thus, for a sufficiently narrow transform F(k), the function \footnotesize \omega(k) can be approximated as a Taylor series around a central frequency \footnotesize \omega_c :
\begin{equation} \omega(k) = \underbrace{\omega(k_c)}_{\omega_c} + (k-k_c)\underbrace{\frac{\partial\omega}{\partial k}\Bigr|_{k=k_c}}_{v_g} , (k>0)\end{equation}
The range k>0 is added because the development is being done with real signals, whose Fourier transforms are hermitian. Therefore the constant terms of the function ω(k) must invert their sign for k<0, as can be seen in the following developments.
Note that the above equation allows to identify the group velocity by complying with equations (11) and (12) obtained in the time domain. However, to complete the demonstration from the frequency domain, equation (15) is substituted into (13), obtaining the following result:
\begin{equation} \begin{split} f(x,t) &= \left(\frac{1}{2\pi}\int F(k)e^{jk(x-v_gt)}e^{j[v_gk_c-\omega_c]t·sgn(k)}dk\right) \\ &= e(x-v_gt,0)·\cos[k_c(x-v_gt)-\varphi(x-v_gt,0)+k_cv_gt-\omega_ct] \\ &= \underbrace{e(x-v_gt,0)}_{\text{envelope}}·\underbrace{\cos(k_cx-\omega_ct-\varphi(x-v_gt,0))}_{\text{carrier}} \end{split}\end{equation}
It is concluded that the envelope propagates at the group velocity \footnotesize v_g as intended to be demonstrated. However, the phase velocity of the signal does not always match the phase velocity of the carrier frequency.
3.2.2 Broad Band Group Velocity
The above result is only valid when the approximation of equation (15) can be performed, as illustrated in Figure 2(a). In that case, equivalent to the one explained in the time-domain demonstration in section 3.1.1, the group velocity is constant.

On the contrary, when it is necessary to include higher order elements of the Taylor series (example in Figure 2(b)), the group velocity is no longer constant for all frequencies and the concept loses physical meaning in line with the explanation in section 3.1.2. A good example of this case is fiber optic propagation, which produces dispersion, and consequently signal distortion [3].
In summary, the function \footnotesize \omega(k) (or \footnotesize k(\omega) ) of a transmission medium is a determining factor in signal propagation.
4. Motion Representation
In this section, moving waves are shown illustrating the concept of group velocity. For simplicity, the simple case obtained in equation (10) is represented, employing constant phase and group velocities \footnotesize v_p and \footnotesize v_g .
The following graph shows three cases: \footnotesize v_p < v_g, \footnotesize v_p = v_g , and \footnotesize v_p > v_g . In all cases the global signal is shown in blue and the group or envelope in red. Also included are red and blue markers that move at the group and phase velocity respectively.

When \footnotesize v_p < v_g the group appears to absorb the wave packets that form at the other end. On the contrary, when \footnotesize v_p > v_g wave packets seem to be overtaking the group in which they form. Finally, when \footnotesize v_p = v_g the group and the wave packets move in unison, remaining unchanged.
For a more complete visualization of the possible scenarios, including distortion, it is recommended to consult this link that deals with signal propagation.
5. Conclusions
The most important conclusions of this article are:
- W. R. Hamilton and Lord Rayleigh can be considered the fathers of the term group velocity. Later researchers such as Sommerfeld and Brillouin refined, modernized and popularized the concept.
- An individual tone or frequency component propagates at phase velocity \footnotesize v_p=\omega/k .
- A bandpass signal consists of a set of frequency components that give rise to a low-frequency envelope with respect to the carrier.
- The group velocity represents the envelope propagation velocity.
- The group velocity formula can be demonstrated in the time and frequency domains resulting in \footnotesize v_g=\partial\omega/\partial k .
- The group velocity can become physically meaningless when it is not constant for all signal components, since dispersion and signal distortion occur.
Bibliography
[1] Communication Systems, A. Bruce Carlson.
[2] Wave Propagation and Group Velocity, Léon Brillouin.
[3] Fiber-Optic Communication Systems, Govind P. Agrawal
Subscription
If you liked this contribution, feel free to subscribe to our newsletter:
