Phase velocity typically denotes the speed with which a sinusoidal wave or tone moves in the medium in which it propagates. The term is coined because the velocity at which the tone moves is equivalent to the speed at which any one of its phases moves, whether it is a phase that produces a zero, a peak, or any value.
Similarly, although with certain reservations, the definition can be extended to the velocity at which a signal composed of multiple tones propagates. In this case the phase velocity can also be understood as the speed at which any phase like a zero or peak propagates, although the peak may vary in amplitude during propagation.
This article first explains conceptually and mathematically the phase velocity of a tone. Subsequently, it goes into the case of signals composed of only two tones, although in favorable conditions to simplify the mathematical calculation. Finally, it is shown how the complexity increases in the case where no degree of freedom is restricted. The table of contents is as follows:
1. Phase Velocity of Sinusoidal Tone
1.1 Context
A tone consists of a sinusoidal wave of amplitude A propagating along the x-axis for a time t:
\begin{equation} f(x,t) = A\cos(kx-\omega t) = A\cos(\omega t - kx) \end{equation}
The explanation of the above equation and its associated parameters are discussed in detail at this link.
1.2 Mathematical Proof
There are several methods to prove the phase velocity vp. Specifically in this section we detail the following proofs: deduction from basic wave parameters, signal delay analysis, and constant phase derivation.
Obviously, in all cases, the same result is obtained:
\begin{equation} v_p = \cfrac{\omega}{k} \end{equation}
1.2.1 Wave Parameters
In the propagation of a tone it is satisfied that the wave travels periodically both in time (period T) and in space (wavelength λ). Therefore the wave travels a wavelength λ during a time period T.
Consequently, the phase velocity vp is deduced as:
\begin{equation} v_p = \cfrac{\lambda}{T} =\cfrac{\omega}{k} \end{equation}
Where the relationships of period T and wavelength λ with oscillation frequency ω and wavenumber k respectively have been applied:
\begin{equation} T = \cfrac{2\pi}{\omega} \end{equation}
\begin{equation}\lambda = \cfrac{2\pi}{k} \end{equation}
1.2.2 Signal Delay
Equation (1) can be written as follows [1]:
\begin{equation} f(x,t) = A\cos\left[\omega \left(t - \frac{x}{\omega / k}\right)\right] =A\cos\left[\omega \left(t - \frac{x}{v_p}\right)\right] \end{equation}
Again it is clear that the tone moves with the phase velocity vp obtained in section 1.2.1.
1.2.3 Constant Phase
Given equation (1), it is possible to define a constant phase value ϕ anywhere between 0 and 2π radians:
\begin{equation} \phi = kx-\omega t \end{equation}
After deducting the variable x we obtain:
\begin{equation} x =\cfrac{\omega t}{k} + \cfrac{\phi}{k} \end{equation}
The phase velocity is the derivative of space x with respect to time t. Therefore:
\begin{equation} v_p =\cfrac{\partial x}{\partial t}= \cfrac{\omega}{k} \end{equation}
1.3 Examples in Motion
After defining and proving the phase velocity, the following graph shows three tones propagating at different velocities:
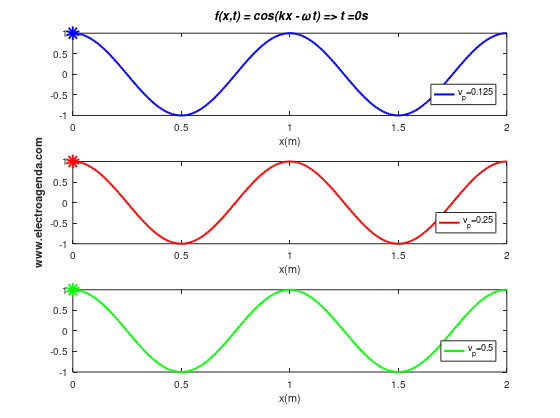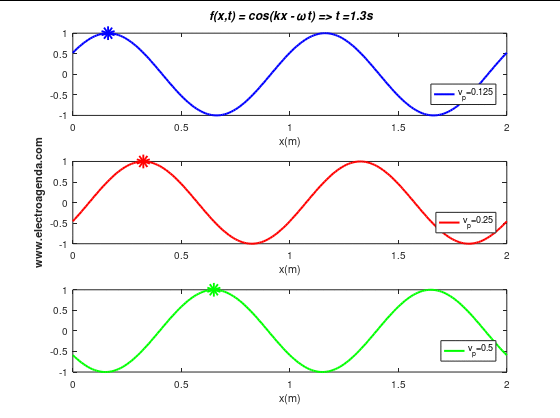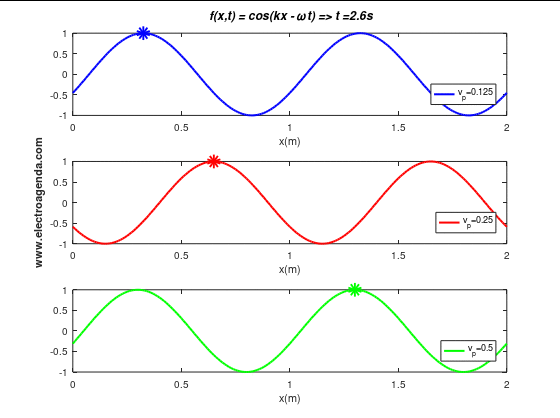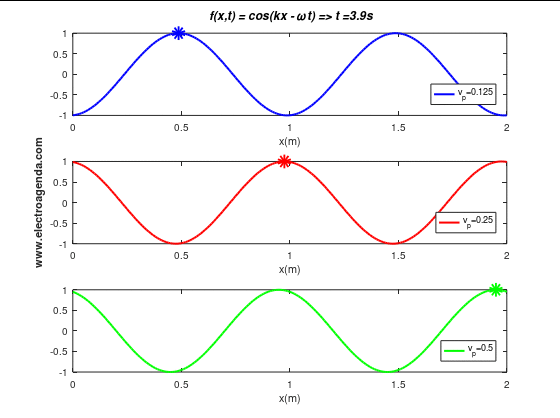
2. Signal Phase Velocity
A signal is typically composed of multiple tones or waves of different frequencies and amplitudes [2]. Obviously this gives rise to different signal waveforms, more complex than a simple sinusoidal tone.
2.1 Approach
2.1.1 General Equation
Mathematically a generic signal propagating in a medium can be expressed as follows:
\begin{equation} s(x,t) = \sum_i A_i \cos(\omega_i t - k_ix) \end{equation}
Where the frequencies and propagation constants can be defined with respect to the respective values at the center frequency (ωc and kc) as follows:
\begin{equation} \omega_i = \omega_c + \Delta\omega_i \end{equation}
\begin{equation} k_i = k_c + \Delta k_i \end{equation}
Note that in equation (10) a generic phase shift at each tone is not added for simplicity, since it does not alter the conclusions of this article.
2.1.2 Calculation
As shown above, the phase velocity is defined for each of the waves composing the signal (vpi=ωi/ki). In the same way, the calculation of the phase velocity for the global signal s(x,t) can be considered. According to Annex A1 (below), it is shown that equation (10) can be written as follows:
\begin{equation} s(x,t) = \underbrace{e(x,t)}_{\text{envelope}}\underbrace{\cos[\omega_c t - k_cx - \varphi(x,t)]}_{\text{carrier}} \end{equation}
This equation is in line with the theory of modulating (or envelope) signals and carriers [2]. While the group velocity is related to the envelope, the phase velocity of the overall signal is related to the carrier. This concept can be easily understood by considering that the carrier forces transmission zeros that propagate at a phase velocity. It also forces transmission peaks that propagate at a phase velocity, although in this case the peaks may change their amplitude during propagation due to the effect of the envelope.
It is shown below that the calculation of the phase velocity of the signal is easily solvable in simple cases, but becomes very complicated when it has to be obtained in a general way for any case.
2.2 Simple Case
The simplest case typically used in the literature to distinguish phase velocity and group velocity in signal propagation theory is explained below.[1].
2.2.1 Mathematical Analysis
This case consists of assuming that the signal is composed of two tones of equal amplitude, but with frequencies and propagation constants (ωi and ki) equidistant to the values of the center frequency (ωc and kc). Mathematically:
\begin{equation}s_{simple}(x,t) = \frac{1}{2}\cos[(\omega_c - \Delta\omega) t - (k_{c}-\Delta k) x] + \frac{1}{2}\cos[(\omega_c + \Delta\omega) t - (k_{c}+\Delta k) x] \end{equation}
Either by using the generic expression in Annex A1 below, or by developing the above equation as shown in this link, the following equality is obtained:
\begin{equation} s_{simple}(x,t) = \underbrace{\cos(\Delta\omega t - \Delta k x)}_{\text{envelope}}·\underbrace{\cos(\omega_c t - k_{c}x)}_{\text{carrier}} \end{equation}
Note that this result coincides with the generic structure shown in equation (13), although allowing a simple calculation of the phase velocity.
2.2.2 Conceptual Analysis
Envelope propagation is discussed in our article on group velocity. This entry, on the other hand, focuses on phase velocity, which is determined by the carrier.
From the analysis of this simple case the following conclusions are obtained. From equation (14) it is evident that the two frequency components that compose the signal can propagate at different phase velocity (vpi=ωi/ki). On the other hand, from equation (15), it is immediate to verify that the phase velocity of the global signal, equivalent to the phase velocity of the carrier, is given by the phase velocity that would have the center frequency (vp=ωc/kc).
Therefore, as long as the k of the medium depends linearly on ω, the above reasoning also applies to signals with symmetric spectra around the carrier. Indeed, each beat consisting of two frequency components (of equal amplitude and equidistant to the carrier) also propagates at the phase velocity of the center frequency.
2.2.3 Representation in Motion
To illustrate this situation, the following moving image is used, in which the global signal and the two frequency components of an example based on equation (14) are observed:

The markers show the different phase velocities of each element (in m/s), being these velocities constant in time and space. In addition, it is observed that the components and the signal propagate at different velocities.
In this case, given the simplicity of the mathematical results, it is easy to calculate the phase velocity of the overall signal, i.e. the velocity at which its zeros (and peaks) propagate. It is clear that this velocity turns out to be the phase velocity that the carrier would have.
Note that the envelope has been included in light blue color simply for aesthetic reasons.
2.3 Advanced Case
Any deviation from the previous case represented in equation (14) results in a significant increase in complexity. Then the calculation of the phase velocity of the global signal is no longer immediate as equations (20) and (22) apply.
The following example shows a small deviation from the previous simple case. The amplitude of the first frequency component is reduced by half, the rest of the parameters remaining unchanged.

It is observed that the phase velocity of the zero marked with the red indicator is no longer constant, as indicated by the graph reading. In general, it can be stated that the phase velocity of each particle of the global signal becomes position and time dependent, vp(x,t), as illustrated in the following video obtained for this same example:

In conclusion, the change in amplitude of one of the components translates into a global phase velocity that is no longer constant. More specifically, the exact calculation of the global phase velocity becomes very complex and it is necessary to apply equations (20) and (22).
3. Phase Velocity Conclusions
The main conclusions of this article are the following:
- The phase velocity represents the propagation velocity of a wave and is given by the expression (vp=ω/k).
- It is called phase velocity because the displacement of the wave is determined by the displacement of any of the phases of the sinusoid.
- The definition can be extended to the phase velocity of a signal composed of multiple tones. In this case the phase velocity of the signal can be understood as the velocity at which the phases of the carrier that multiplies the envelope propagate.
- While the calculation of the phase velocity of a tone is immediate, the phase velocity of a signal is only easily obtained in simple cases.
Annex A1: Generic Phase Velocity Calculation
A1.1 Generic Starting Point
The starting point is given by equations (10), (11), and (12). Strictly speaking, in equation (10) a constant phase shift, which could be different for each frequency, should be introduced . This phase shift is not included because it results in more complexity but does not alter the conclusions of this text.
A1.2 Mathematical Development
Rearranging terms gives:
\begin{equation} s(x,t) = \sum_i A_i \cos[ (\omega_c t - k_cx)+(\Delta\omega_i t - \Delta k_ix)] \end{equation}
The following trigonometric equality is applied:
\begin{equation} \cos(a+b) = \cos(a)\cos(b)-\sin(a)\sin(b) \end{equation}
Obtaining the following result:
\begin{equation} \begin{split} s(x,t) &=\sum_i A_i \cos(\Delta\omega_i t - \Delta k_ix)\cos(\omega_c t - k_cx)\\ &-\sum_i A_i \sin(\Delta\omega_i t - \Delta k_ix)\sin(\omega_c t - k_cx) \end{split} \end{equation}
The objective is to calculate the phase velocity. Hence a sinusoidal term must be obtained that depends on the center frequency and multiplies the signal envelope. Consequently the following trigonometric equality (obtained from this link) is applied:
\begin{equation} A\cos(\omega t) + B\sin(\omega t) = \sqrt{A^2+B^2}\cos\left[\omega t - \arctan\left(\cfrac{B}{A}\right)\right] \end{equation}
And the final result is obtained:
\begin{equation} s(x,t) = \underbrace{e(x,t)}_{\text{envelope}}\underbrace{\cos[\omega_c t - k_cx - \varphi(x,t)]}_{\text{carrier}} \end{equation}
\begin{equation} e(x,t) = \sqrt{\left[\sum_i A_i \cos(\Delta\omega_i t - \Delta k_ix)\right]^2+\left[\sum_i A_i \sin(\Delta\omega_i t - \Delta k_ix)\right]^2} \end{equation}
\begin{equation} \varphi(x,t) = \arctan\left(\cfrac{-\sum_i A_i \sin(\Delta\omega_i t - \Delta k_ix)}{\sum_i A_i \cos(\Delta\omega_i t - \Delta k_ix)}\right) \end{equation}
A1.3 Results Analysis
Equation (21) allows to generalize the group velocity equation for a signal composed of multiple tones. However, equation (22) shows that the phase velocity of the overall signal cannot be generalized.
If any reader would like to comment on or contribute to the improvement of this article, please let us know in the following link.
Bibliography
[1]Wave Propagation and Group Velocity, Léon Brillouin.
[2] Communication Systems, A. Bruce Carlson.
Subscription
If you liked this contribution, feel free to subscribe to our newsletter:
