Las modulaciones de envolvente constante son de vital importancia en las radiocomunicaciones debido a limitaciones de los componentes electrónicos. En práctica es necesario analizar no solo los símbolos de una modulación, sino también las transiciones entre ellos.
Por ejemplo, en una modulación QPSK, todos los símbolos tienen envolvente constante, pero existen transiciones entre ellos donde la envolvente se desvanece. Este fenómeno se puede enmendar empleando offset-QPSK (OQPSK), donde todas las transiciones entre símbolos mantienen la envolvente «prácticamente» constante.
Este texto repasa brevemente la importancia de la envolvente constante para, posteriormente, explicar las diferencias entre QPKS y OQPSK, tanto a nivel de símbolo como a nivel de sus transiciones. El índice de contenidos es el siguiente:
1. ¿Por qué se necesita Envolvente Constante?
En comunicaciones de RF y microondas [1][2], es necesario utilizar amplificadores de potencia, tanto de estado sólido como tubos, que no operan de una forma puramente lineal. Por motivos de eficiencia energética, estos amplificadores suelen trabajar en zona saturada [3][4], lo que implica distintos tipos de distorsión [5][6]. En primer lugar, alteración entre la relación de amplitud y fase de la señal. En segundo lugar, expansión del espectro de la señal.
Por la primera deficiencia, se descartan modulaciones como QAM, puesto que envían la información usando tanto la amplitud como la fase de la señal [7]. En su lugar es preferible usar modulaciones de envolvente constante, como QPSK u OQPSK, que envían la información únicamente en la fase de la señal [7]. Además, para reducir la segunda deficiencia (expansión espectral), es necesario que la envolvente permanezca idealmente constante también en las transiciones entre símbolos. Por este motivo, OQPSK se prefiere a QPSK.
2. QPSK vs OQPSK
A continuación se profundiza en las modulaciones QPSK y OQPSK, tanto a nivel matemático como a nivel gráfico usando el plano complejo [8]. Para una comprensión más profunda del texto se recomienda leer los siguientes enlaces sobre la Transformada de Hilbert, la señal analítica, y la envolvente compleja.
Las señales empleadas en este artículo seguirán, por tanto, la estructura basada en componentes en fase i(t) y cuadratura q(t) [5][6][7]:
\begin{equation} s(t) = i(t)\cos{\left(\omega_c t \right)} + q(t)\sin{\left(\omega_c t \right)} \end{equation}
2.1 Representación Matemática
QPSK, del inglés Quaternaty Phase Shift Keying, emplea cuatro símbolos de la misma amplitud y frecuencia, que se distinguen por su fase [7].
Matemáticamente, siguiendo la notación expresada arriba:
\begin{equation} i(t)_{QPSK} = \sum_{\mathclap{n}} a_{I_n}p(t-nT_s) \end{equation}
\begin{equation} q(t)_{QPSK} = \sum_{\mathclap{n}} a_{Q_n}p(t-nT_s) \end{equation}
\begin{equation} a_{I_n} = (+1 , -1) , a_{Q_n} = (+1 , -1) \end{equation}
Donde p(t) es una pulso rectangular con duración igual al tiempo de símbolo Ts. Y aIn y aQn representan en conjunto el enésimo símbolo, con cuatro combinaciones posibles: (-1,-1), (-1,+1), (+1,-1), y (+1,+1). Notar que estos últimos valores se están usando por simplicidad. En función de la potencia de la señal deseada, habría que redimensionar las amplitudes de los símbolos.
Por otra parte, en OQPSK, del inglés offset QPSK, existe una sutil diferencia. Concretamente, el símbolo en cuadratura varía a mitad del período de símbolo con respecto al símbolo en fase. Matemáticamente:
\begin{equation} i(t)_{OQPSK} = \sum_{\mathclap{n}} a_{I_n}p(t-nT_s) \end{equation}
\begin{equation} q(t)_{OQPSK} = \sum_{\mathclap{n}} a_{Q_n}p\left[t-\left(n+\cfrac{1}{2}\right)T_s\right] \end{equation}
Las consecuencias de esta pequeña diferencia son notables, pero se explicarán en el siguiente apartado para ayudarse de la representación gráfica en el plano complejo.
2.2 Representación en Plano Complejo
A continuación, se ilustran las constelaciones QPSK y OQPSK en el plano complejo:
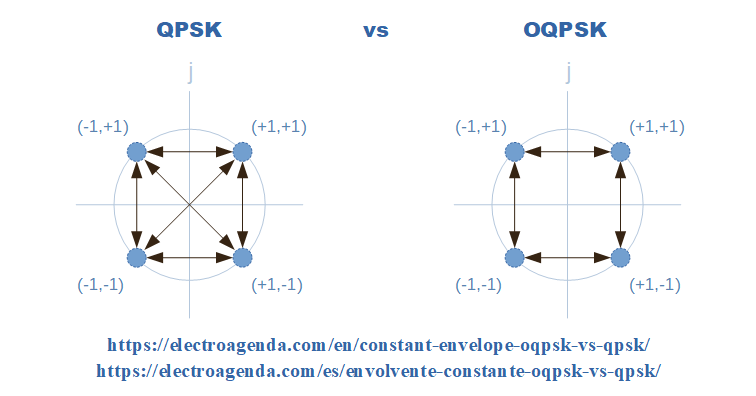
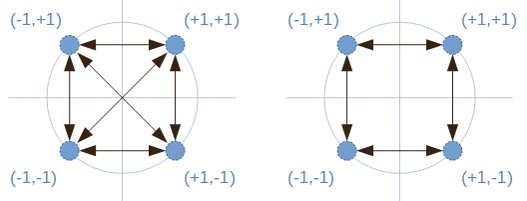
Como es lógico, ambas constelaciones presentan cuatro posibles símbolos, derivados de las posibilidades otorgadas por las componentes en fase y cuadratura. Todos los símbolos tienen la misma envolvente, concretamente el módulo del vector que va desde el origen de coordenadas hasta el símbolo.
Las flechas entre símbolos representan las transiciones entre ellos. Cada constelación se analiza por separado:
- En QPSK, existen transiciones que implican un cambio de fase de 180º. Son los casos en que las amplitudes de las componentes en fase y cuadratura cambian simultáneamente su polaridad, por ejemplo el paso de (+1,+1) a (-1,-1). Durante tal evento, existe un punto en el que ambas componentes pasan por el origen de coordenadas, lo que implica que la envolvente de la señal es cero.
- En cambio, en OQPSK no existen transiciones que cambien la polaridad de las componentes en fase y cuadratura simultáneamente. Como ambas ramas varían en instantes diferentes, cada salto se produce necesariamente a uno de los símbolos contiguos. Por lo tanto, las transiciones entre símbolos mantienen una envolvente más parecida a la del símbolo, que no se desvanece como en QPSK.
Por último, notar que en algunas ocasiones se tiende a representar la constelación OQPSK con una rotación de 45º respecto a la que se observa en la figura. Los razonamientos aquí presentados son igualmente válidos en ambas representaciones.
3 Transiciones entre Símbolos
Esta sección ilustra mediante animaciones (generadas con MATLAB u Octave [9]) las transiciones entre símbolos tanto en QPSK como en OQPSK. Para todos los casos se emplearán cuatro períodos de la portadora por símbolo. Además, para que las transiciones sean más apreciables, se exagerarán alargándose todo un tiempo de símbolo. Finalmente, por simplicidad, se emplean pulsos cuadrados.
3.1 Envolvente Constante de Símbolo (QPSK)
A continuación se ilustra una transición entre símbolos con cambio de polaridad en QPSK. La transición ha sido alargada durante toda la duración de un símbolo para que sea más apreciable el desvanecimiento de la envolvente.
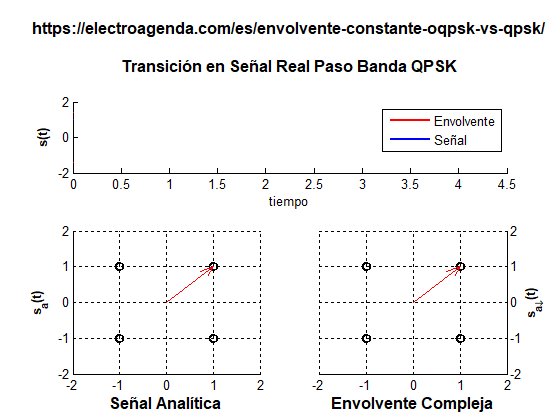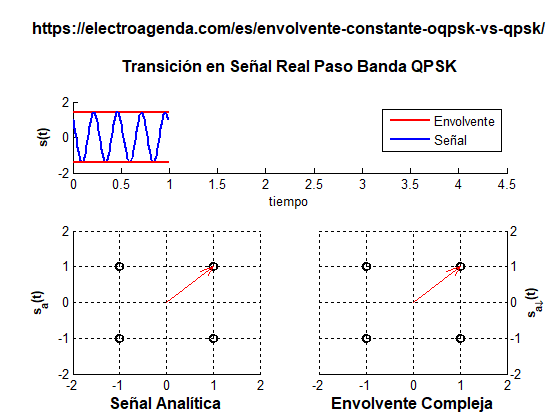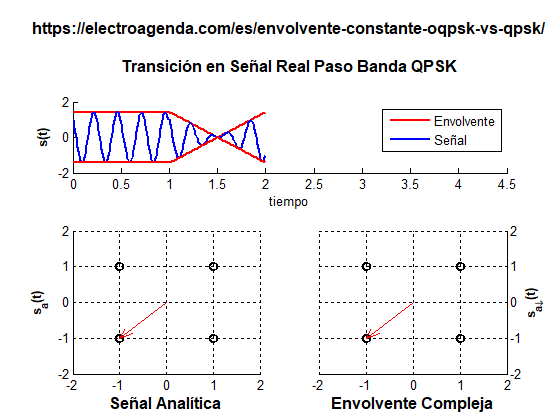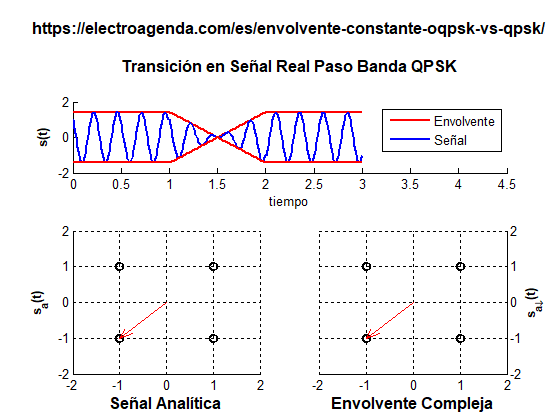
Mientras se pasa del símbolo (+1,+1) al símbolo (-1,-1), la envolvente debe cruzar por el origen de coordenadas, punto en el que la envolvente se ha desvanecido completamente. En un caso realista este efecto sería mucho más rápido que en la animación, puesto que la transición duraría solo una fracción del tiempo de símbolo. Pero igualmente se produciría un desvanecimiento instantáneo de la envolvente.
En resumen, aunque QPSK se trate de una modulación donde todos los símbolos presentan envolvente constante, la transición entre los símbolos puede producir un desvanecimiento temporal de la envolvente. Este efecto es incompatible con muchas aplicaciones, como se ha explicado en el punto 1.
3.2 Envolvente Constante de Símbolo y Transición (OQPSK)
A continuación se ilustra una serie de transiciones entre símbolos con OQPSK. Para que se produzca un cambio de polaridad, es necesario hacer dos saltos entre símbolos. Ambas transiciones producidas por estos saltos han sido alargadas durante toda la duración de un símbolo para que sean más apreciables.
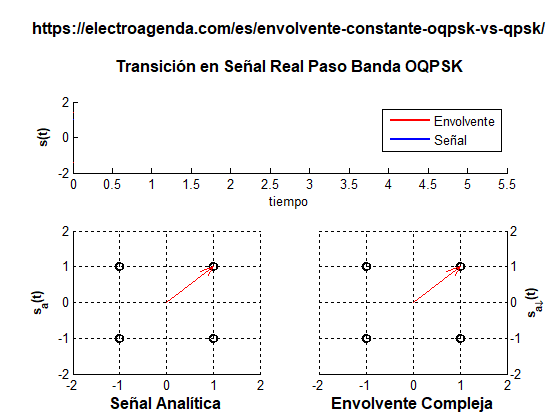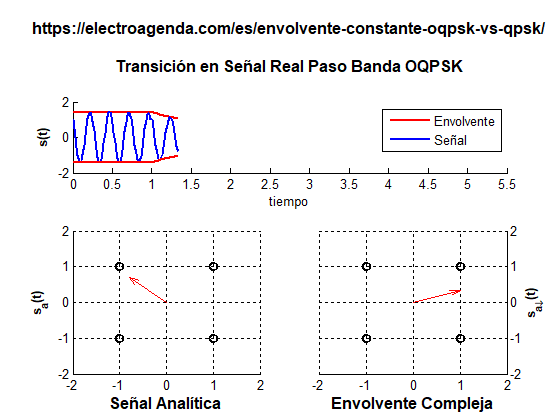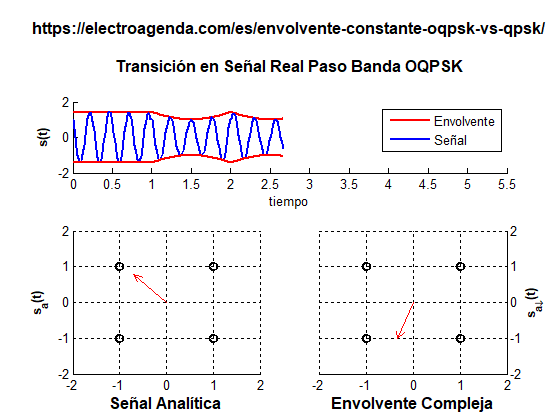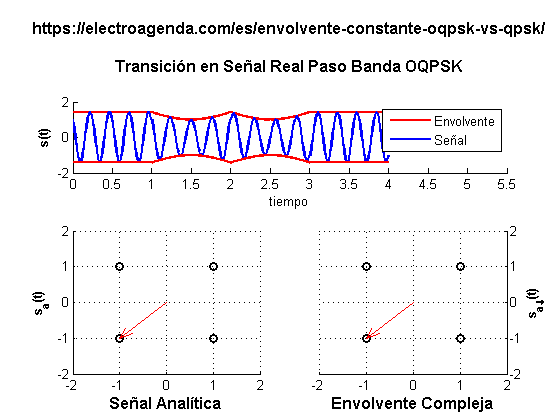
Para pasar del símbolo (+1,+1) al símbolo (-1,-1), se producen dos saltos, usando el símbolo (+1,-1) como paso intermedio. En este caso, la envolvente no cruza por el origen de coordenadas, por lo que no se desvanece en ningún momento.
En práctica, como se observa en la animación, el valor de la envolvente durante la transición no es constante. Por ejemplo, en el primer salto existe un punto de mínima envolvente (+1,0) que es lógicamente inferior a la envolvente de símbolo. En un caso realista, donde las transiciones duran solo una fracción del tiempo de símbolo, este efecto apenas es apreciable, a diferencia de los desvanecimientos completos de envolvente que se dan en QPSK.
En resumen, OQPSK es una modulación de envolvente constante de símbolo, al igual que QPSK. Sin embargo, cuando la envolvente se debe mantener en todo momento incluyendo las transiciones entre símbolos, OQPSK es superior y preferida a QPSK.
4. Conclusiones
Las conclusiones de este texto son las siguientes:
- Por la zona de trabajo saturada de determinados amplificadores de potencia, es necesario utilizar modulaciones donde todos los símbolos presentan envolvente constante, como QPSK u OQPSK.
- Para evitar expansión espectral, es necesario que la envolvente constante se mantenga constante también durante las transiciones entre símbolos, característica en la que OQPSK en superior a QPSK.
- En QPSK, las transiciones entre símbolos producen desvanecimientos completos de la envolvente cuando existe un cambio de polaridad simultáneo en las ramas en fase y cuadratura.
- En OQPSK, las ramas en fase y cuadratura no varían simultáneamente. En consecuencia, no se pueden producir transiciones entre símbolos donde la envolvente se desvanezca.
Bibliografía (Patrocinado)
[1] Microwave Engineering, Pozar
[2] RF Circuit Design, Bowick
[3] Electronic Principles, Malvino
[4] Electrónica, Hambley
[5] Communication Systems, Carlson
[6] Signals and Systems, Openheim
[7] Digital Communications, Sklar
[8] Understanding Digital Signal Processing, Lyons
[9] Guía de MATLAB/Octave
Subscripción
Si te ha gustado esta publicación, nos encantaría que te suscribas a nuestro boletín: