Contributions related to the theory of signal transmission systems. Also directly applicable to electronics, especially communications electronics.
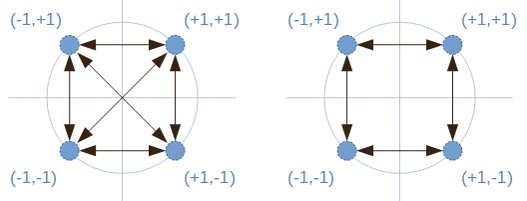
Constant envelope modulations are of vital importance in radio communications due to limitations of electronic components. In practice it is necessary to analyze not only the symbols of a modulation, but also the transitions between them. For example, in a QPSK modulation, all symbols have constant envelope, but there are transitions between them where the […]
The envelope of a bandpass signal represents the signal, typically baseband, that served as the modulator of the carrier frequency. Although the power of the resulting signal may vary with time, its value can be generalized as a function of the envelope amplitude. The following text shows the evolution from the calculation of the power […]
Complex numbers extend the real numbers by adding an additional term called imaginary. This two-dimensionality makes it possible to simplify the understanding and calculations of many mathematical and physical questions. This article explains the basic fundamentals of complex numbers and their main applications for the particular case of electronics [1][2] and communications [3][4]. The table […]
The complex envelope is a baseband analytic signal. It is obtained by suppressing the negative (or positive) frequencies of a real bandpass signal, and transferring the remaining spectral content to baseband. Due to the complex notation and the spectral efficiency of the resulting signal, the complex envelope is very useful in both linear system simulation […]
The analytic signal is a complex representation of a real signal, obtained by suppressing the negative frequency components of the original signal. From the analytic signal is derived the equivalent baseband signal, also an analytic representation known as complex envelope. Both representations are used in signal processing techniques due to their main advantages: spectral efficiency […]
The mathematics of linear distortion only applies to linear and time invariant systems [1] [2]. Therefore, these systems and their translation to the frequency domain, where the mathematical analysis is simplified, are briefly summarized. Then it is discussed how the presented theory can be applied to real transmission media and/or electronic components. Finally, the mathematics […]
The Hilbert transform is a linear operation applied to real signals. In practical terms, the Hilbert transform translates into a phase shift of -90º at the positive frequencies (and +90º at the negative frequencies) that make up the signal. The relevance of the Hilbert transform in telecommunication engineering is due to its contribution in obtaining […]
The Fourier transform makes it possible to obtain the components that make up a signal in the transformed domain. In the most common case, the Fourier transform of temporal signals provides the frequencies (ω) that make up the signal. Equivalently, the spatial Fourier transform, applied on a signal defined in space, provides its components typically […]
In communications, signal propagation theory studies the movement of signals from the transmitter to the receiver through a transmission medium. Depending on the characteristics of the signal and the medium, different situations may arise. In general, the cases are classified according to the type of distortion they produce in the transmitted signal. This text is […]
Phase velocity typically denotes the speed with which a sinusoidal wave or tone moves in the medium in which it propagates. The term is coined because the velocity at which the tone moves is equivalent to the speed at which any one of its phases moves, whether it is a phase that produces a zero, […]