Constant envelope modulations are of vital importance in radio communications due to limitations of electronic components. In practice it is necessary to analyze not only the symbols of a modulation, but also the transitions between them.
For example, in a QPSK modulation, all symbols have constant envelope, but there are transitions between them where the envelope vanishes. This phenomenon can be amended by using offset-QPSK (OQPSK), where all transitions between symbols keep the envelope “practically” constant.
This text briefly reviews the importance of the constant envelope and then explains the differences between QPKS and OQPSK, both at the symbol level and at the level of their transitions. The table of contents is as follows:
1. Why is Constant Envelope needed?
In RF and microwave communications [1][2], it is necessary to use power amplifiers, both solid-state and tube, which do not operate in a purely linear state. For energy efficiency reasons, these amplifiers usually work in saturated zone [3][4], which implies different types of distortion [5][6]. Firstly, alteration between the amplitude and phase relationship of the signal. Secondly, expansion of the signal spectrum.
Because of the first shortcoming, modulations such as QAM are discarded, since they send the information using both the amplitude and the phase of the signal [7]. Instead, it is preferable to use constant envelope modulations, such as QPSK or OQPSK, which send the information only in the phase of the signal [7]. Moreover, to reduce the second deficiency (spectral expansion), it is necessary that the envelope remains ideally constant also in the transitions between symbols. For this reason, OQPSK is preferred to QPSK.
2. QPSK vs OQPSK
Next, QPSK and OQPSK modulations are discussed in depth, both mathematically and graphically using the complex plane [8]. For a deeper understanding of the text it is recommended to read the following links on the Hilbert Transform, the analytic signal, and the complex envelope.
The signals used in this article will therefore follow the structure based on in-phase i(t) and quadrature q(t) components [5][6][7]:
\begin{equation} s(t) = i(t)\cos{\left(\omega_c t \right)} + q(t)\sin{\left(\omega_c t \right)} \end{equation}
2.1 Mathematical Representation
QPSK, which stands for Quaternaty Phase Shift Keying, uses four symbols of the same amplitude and frequency, which are distinguished by their phase [7].
Mathematically, following the above notation:
\begin{equation} i(t)_{QPSK} = \sum_{\mathclap{n}} a_{I_n}p(t-nT_s) \end{equation}
\begin{equation} q(t)_{QPSK} = \sum_{\mathclap{n}} a_{Q_n}p(t-nT_s) \end{equation}
\begin{equation} a_{I_n} = (+1 , -1) , a_{Q_n} = (+1 , -1) \end{equation}
Where p(t) is a rectangular pulse with duration equal to the symbol time Ts. And aIn and aQn together represent the nth symbol, with four possible combinations: (-1,-1), (-1,+1), (+1,-1), and (+1,+1). Note that these last values are being used for simplicity. Depending on the power of the desired signal, the symbol amplitudes should be resized.
On the other hand, in OQPSK, which stands for offset QPSK, there is a subtle difference. Specifically, the quadrature symbol varies at half the symbol period with respect to the in-phase symbol. Mathematically:
\begin{equation} i(t)_{OQPSK} = \sum_{\mathclap{n}} a_{I_n}p(t-nT_s) \end{equation}
\begin{equation} q(t)_{OQPSK} = \sum_{\mathclap{n}} a_{Q_n}p\left[t-\left(n+\cfrac{1}{2}\right)T_s\right] \end{equation}
The consequences of this small difference are remarkable, but will be explained in the following section using the graphical representation in the complex plane.
2.2 Complex Plane Representation
The QPSK and OQPSK constellations are illustrated below in the complex plane:
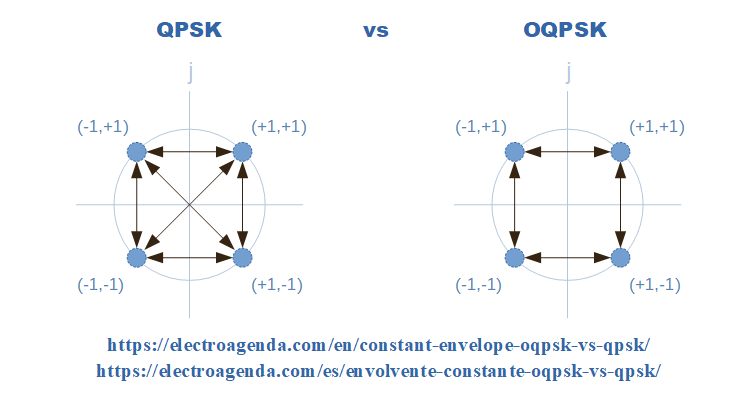
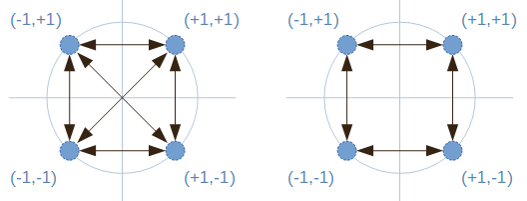
As is logical, both constellations present four possible symbols, derived from the possibilities granted by the in phase and quadrature components. All symbols have the same envelope, namely the modulus of the vector from the origin of coordinates to the symbol.
The arrows between symbols represent the transitions between them. Each constellation is analyzed separately:
- In QPSK, there are transitions that involve a 180º phase change. These are the cases in which the amplitudes of the in-phase and quadrature components simultaneously change their polarity, for example the transition from (+1,+1) to (-1,-1). During such an event, there is a point where both components pass through the origin of coordinates, which implies that the signal envelope is zero.
- In contrast, in OQPSK there are no transitions that change the polarity of the in-phase and quadrature components simultaneously. Since both branches vary at different times, each jump is necessarily to one of the adjacent symbols. Therefore, the transitions between symbols maintain a closer envelope to that of the symbol, which does not fade as in QPSK.
Finally, note that sometimes the OQPSK constellation tends to be represented with a 45º rotation with respect to the one shown in the figure. The rationale presented here is equally valid in both representations.
3 Symbol Transitions
This section illustrates by means of animations (generated with MATLAB or Octave [9]) the transitions between symbols in both QPSK and OQPSK. For all cases, four carrier periods per symbol will be used. In addition, to make the transitions more noticeable, they will be exaggerated and lengthened for an entire symbol time. Finally, for simplicity, square pulses are used.
3.1 Symbol Constant Envelope (QPSK)
A transition between QPSK symbols with polarity change is illustrated below. The transition has been lengthened for the entire duration of a symbol to make the fading of the envelope more noticeable.
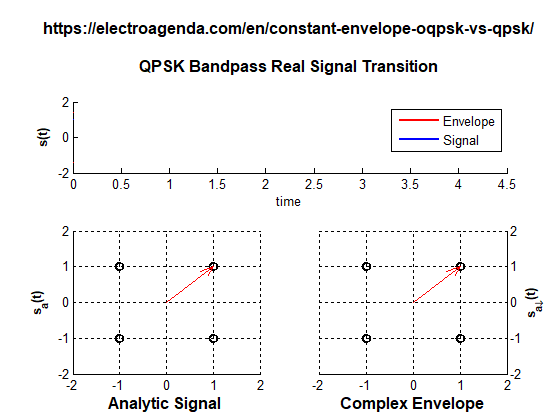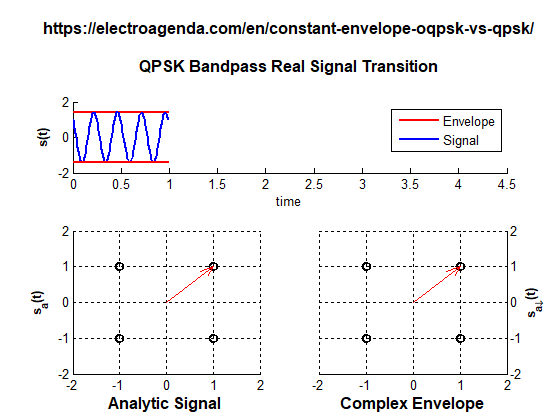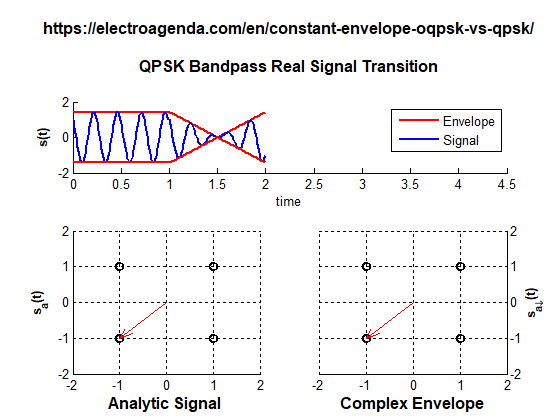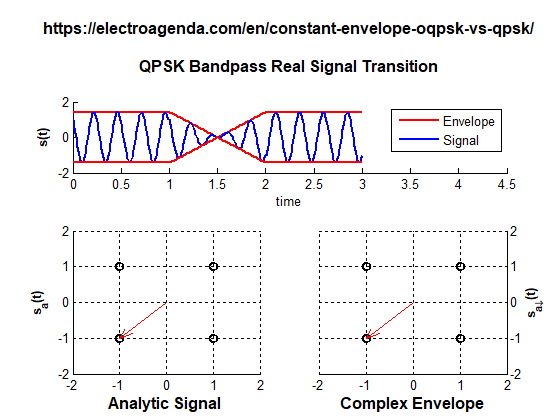
While transitioning from symbol (+1,+1) to symbol (-1,-1), the envelope must cross the coordinates origin, at which the envelope has completely vanished. In a realistic case this effect would be much faster than in the animation, since the transition would last only a fraction of the symbol time. But there would still be an instantaneous fading of the envelope.
In summary, although QPSK is a modulation where all symbols have a constant envelope, the transition between symbols can produce a temporary fading of the envelope. This effect is incompatible with many applications, as explained in section 1.
3.2 Symbol and Transition Constant Envelope (OQPSK)
A series of transitions between OQPSK symbols is illustrated below. For a polarity change to occur, two inter-symbol jumps are required. Both transitions produced by these jumps have been stretched over the entire duration of a symbol to make them more noticeable.
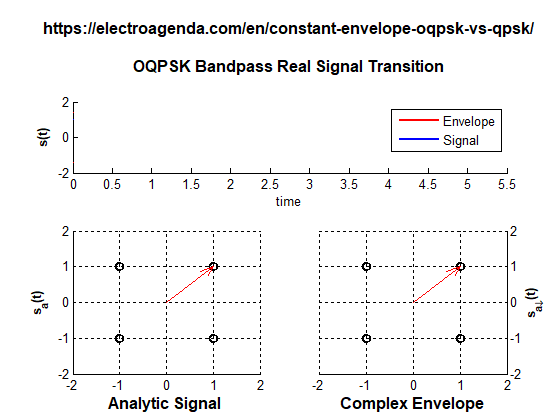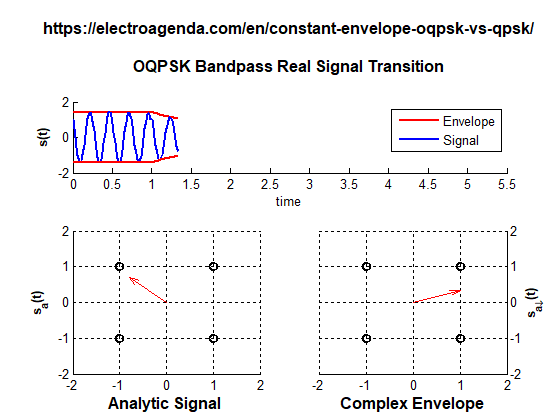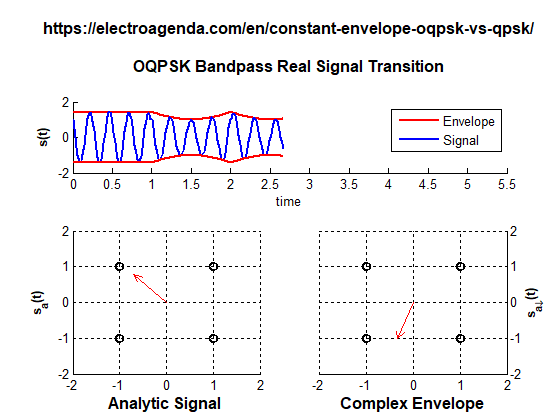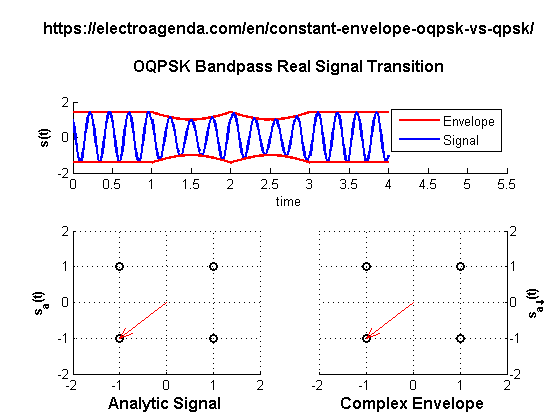
To go from the symbol (+1,+1) to the symbol (-1,-1), two jumps are made, using the symbol (+1,-1) as an intermediate step. In this case, the envelope does not cross the origin of coordinates, so it does not vanish at any time.
In practice, as can be seen in the animation, the value of the envelope during the transition is not constant. For example, at the first jump there is a point of minimum envelope (+1,0) which is logically lower than the symbol envelope. In a realistic case, where transitions last only a fraction of the symbol time, this effect is hardly noticeable, unlike the complete envelope fades that occur in QPSK.
In summary, OQPSK is a constant symbol envelope modulation, just like QPSK. However, when the envelope must be maintained at all times including transitions between symbols, OQPSK is superior and preferred to QPSK.
4. Conclusions
The conclusions of this text are as follows:
- Due to the saturated working area of certain power amplifiers, it is necessary to use modulations where all symbols have a constant envelope, such as QPSK or OQPSK.
- To avoid spectral expansion, it is necessary that the constant envelope remains constant also during the transitions between symbols, a feature in which OQPSK is superior to QPSK.
- In QPSK, inter-symbol transitions produce complete envelope fades when there is a simultaneous polarity change in the in-phase and quadrature branches.
- In OQPSK, the in-phase and quadrature branches do not vary simultaneously. Consequently, transitions between symbols where the envelope fades cannot occur.
Bibliography (Patrocinado)
[1] Microwave Engineering, Pozar
[2] RF Circuit Design, Bowick
[3] Electronic Principles, Malvino
[4] Electronics, Hambley
[5] Communication Systems, Carlson
[6] Signals and Systems, Openheim
[7] Digital Communications, Sklar
[8] Understanding Digital Signal Processing, Lyons
[9] MATLAB/Octave Guide
Subscription
If you liked this contribution, do not hesitate to subscribe to our newsletter: