Los números complejos extienden los números reales mediante la suma de un término adicional que se denomina imaginario. Esta bidimensionalidad permite simplificar la comprensión y los cálculos de muchas cuestiones matemáticas y físicas.
Este artículo explica los fundamentos básicos de los números complejos y sus aplicaciones principales para el caso particular de la electrónica [1][2] y las comunicaciones [3][4]. El índice de contenidos es el siguiente:
1. Fundamentos de Números Complejos
Este apartado sienta las bases para una correcta comprensión de la relevancia de los números complejos en electrónica [1][2] y comunicaciones [3][4]. Tras una concisa explicación de la teoría más genérica, se introduce la Fórmula de Euler y su relación con las funciones trigonométricas básicas, seno y coseno. Con este conocimiento se desvelan las posibles representaciones de un número complejo, cuya elección es clave para resolver más fácilmente los cálculos matemáticos necesarios en cada aplicación.
1.1 Definición
Un número complejo se obtiene mediante la suma de dos elementos: un término real y uno imaginario. Como su propio nombre indica, la parte real consta de un número real. En cambio, la parte imaginaria se obtiene al multiplicar un número real por el operador imaginario j. Por ejemplo, siendo a y b dos números reales, el siguiente número, c, es complejo:
\begin{equation} c = a + jb \end{equation}
Notar que en la literatura se suele representar al operador imaginario con la letra i. Sin embargo, en el contexto de la electrónica se emplea la letra j, porque la letra i esta reservada para la intensidad o corriente de una rama en un circuito.
1.2 El Operador j
Hasta aquí todo parece sencillo. Ahora llega el punto en el que se produce un salto didáctico que ni siquiera los matemáticos más ilustres pueden desvelar completamente. ¿Qué demonios es el operador j? Iré al grano:
\begin{equation} j = \sqrt{-1} \end{equation}
Pero…. un momento. ¿Qué número multiplicado por sí mismo permite obtener un valor negativo? Incluso un niño de primaria sabe que cualquier número, positivo o negativo, multiplicado por sí mismo produce un valor positivo.
La realidad es que no sabemos muy bien qué es el operador j. Sí que conocemos su origen, concretamente es una raíz del polinomio x2+1. Y, en general, podemos extender que los números complejos son raíces no reales de polinomios.
De momento vamos a continuar, asumiendo que el operador j simplemente existe aunque no lo sepamos explicar muy bien. Como veremos, las operaciones aritméticas con el operador j encajan sin ambigüedades. De forma similar, los físicos también emplean conceptos de elementos que no han visto, pero cuyas propiedades se manifiestan de forma consistente con sus principios matemáticos.
Más abajo veremos que el operador j tiene un sentido espacial en el plano complejo. Concretamente, desplazar 90º en sentido contrario a las agujas del reloj. Esperemos que esta utilidad pueda resultar un cierto alivio para el lector más riguroso.
1.3 Fórmula de Euler
En este apartado damos un paso más en la extravagante aritmética de los números complejos. Herr Leonard Euler descubrió una fórmula que, por decirlo finamente, no resulta muy intuitiva. Concretamente:
\begin{equation} e^{j\phi} = \cos(\phi)+j\sin(\phi) \end{equation}
En este apartado se demuestra la fórmula y se obtienen sus derivaciones más relevantes. Este conocimiento se usará más abajo para atribuirle un sentido más nemotécnico al operador j.
1.3.1 Demostración Matemática
La demostración comienza recordando la siguiente serie de Taylor:
\begin{equation} e^{z} = 1+z+\cfrac{z^2}{2!}+\cfrac{z^3}{3!}+\cfrac{z^4}{4!}+\cfrac{z^5}{5!}+\cfrac{z^6}{6!}+... \end{equation}
Como z representa cualquier número complejo, se puede evaluar la función en z=jϕ, resultando en:
\begin{equation} e^{j\phi} = 1+j\phi-\cfrac{{\phi}^2}{2!}-j\cfrac{{\phi}^3}{3!}+\cfrac{{\phi}^4}{4!}+j\cfrac{{\phi}^5}{5!}-\cfrac{{\phi}^6}{6!}+... \end{equation}
Reordenando términos, y aplicando las igualdades de Taylor del seno y el coseno, se demuestra la ecuación (3):
\begin{equation} e^{j\phi} = \underbrace{1-\cfrac{{\phi}^2}{2!}+\cfrac{{\phi}^4}{4!}-\cfrac{{\phi}^6}{6!}+...}_{\cos(\phi)}+j\underbrace{\left(\phi-\cfrac{{\phi}^3}{3!}+\cfrac{{\phi}^5}{5!}+...\right)}_{\sin(\phi)} \end{equation}
1.3.2 Derivaciones Importantes
A continuación reescribimos la fórmula de Euler usando el ángulo tanto con signo positivo como con signo negativo. Usando trigonometría básica se deduce que:
\begin{equation} e^{j\phi} = \cos(\phi)+j\sin(\phi) \end{equation}
\begin{equation} e^{-j\phi} = \cos(\phi)-j\sin(\phi) \end{equation}
Sumando y restando las ecuaciones anteriores, y reordenando términos, se obtienen dos resultados importantísimos. Concretamente se consiguen definir las funciones reales coseno y seno, en función de números complejos:
\begin{equation} \cos(\phi) = \cfrac{e^{j\phi} + e^{-j\phi}}{2} \end{equation}
\begin{equation} \sin(\phi) = \cfrac{e^{j\phi} - e^{-j\phi}}{2j} \end{equation}
Resumiendo, una sinusoide real se puede representar en el plano complejo empleando exponenciales complejas. De estas igualdades se puede derivar la representación de señales reales en el dominio de la frecuencia [3][5].
1.4 El Plano Complejo
A continuación se introduce el plano complejo a partir de la Fórmula de Euler. Además, las posibles representaciones de los números complejos se derivan matemáticamente y gráficamente a partir de la visualización de dicho plano complejo.
1.4.1 Significado Gráfico de j
Típicamente, en la literatura se muestra el plano complejo vectorial nada mas introducir la teoría de la parte imaginaria de los números complejos. En este texto usamos una aproximación diferente. Para que el plano complejo aparezca como un concepto lógico y no arbitrario, el texto se apoya en la fórmula de Euler.
En efecto, matemáticamente a partir de la ecuación (3), es inmediato deducir que cualquier numero real b multiplicado por j implica un desfase de 90º respecto al valor b original:
\begin{equation} be^{\frac{j\pi}{2}} = b\left[\cos\left(\cfrac{\pi}{2}\right)+j\sin\left(\cfrac{\pi}{2}\right)\right]=bj \end{equation}
Haciendo b=1=e^{j0} , y comparando con j=e^{\frac{j\pi}{2}} , queda claro que el operador j está desfasado 90º respecto a la unidad real. Y, explicado de forma más genérica, la parte imaginaria de un número complejo debe ser ortogonal a la parte real. Por lo tanto, el número complejo c=a+jb se representa en el plano complejo como muestra la siguiente imagen:
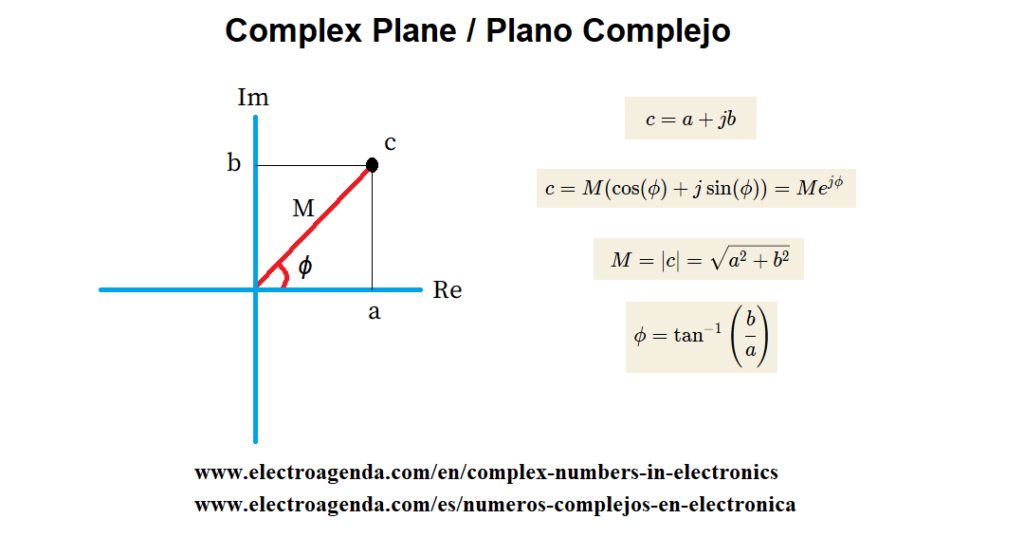
Analizando la gráfica se pone de manifiesto que el operador j implica un desfase de 90º en sentido contrario a las agujas del reloj. De forma que ambos partes, real e imaginaria, son ortogonales porque los ejes en los que se sitúan forman un ángulo de 90º.
1.4.2 Expresiones Equivalentes
A partir de la gráfica anterior, empleando trigonometría básica, se puede deducir que el número complejo c es igual a:
\begin{equation} c = M(\cos(\phi)+j\sin(\phi))=Me^{j\phi} \end{equation}
Donde M es el módulo del número complejo y ϕ representa la fase:
\begin{equation} M = |c| = \sqrt{a^2 + b^2} \end{equation}
\begin{equation} \phi = \tan^{-1}\left(\cfrac{b}{a}\right) \end{equation}
En resumen, la siguiente tabla muestra las distintas formas de escribir o representar el número complejo c:
| Notación | Expresión |
| Cartesiana | \begin{equation} c = a+jb \end{equation} |
| Trigonométrica | \begin{equation} c = M(\cos(\phi)+j\sin(\phi)) \end{equation} |
| Polar | \begin{equation} c = Me^{j\phi} \end{equation} |
| Módulo-Ángulo | \begin{equation} c = M\phase\phi \end{equation} |
2. Aplicaciones de los Números Complejos
Las aplicaciones de los números complejos en electrónica [1][2] y comunicaciones [3][4] se articulan en base a la definición del fasor, representación matemática de un tono que permite simplificar los cálculos y la comprensión de múltiples conceptos.
Una de las aplicaciones típicas es la teoría de circuitos [2], donde los fasores permiten analizar de forma sencilla el régimen permanente sinusoidal. Además, el uso de fasores se puede generalizar al análisis de señales, compuestas por múltiples tonos, en cualquier sistema lineal. De ahí la relevancia de los números complejos en la teoría de señal [3][4] y comunicaciones [6].
2.1 Fasores
Un fasor es un número complejo que representa un tono o sinusoide de amplitud y fase fijos e invariantes en el tiempo. A continuación se desarrolla la representación matemática y gráfica de este concepto.
2.1.1 Representación Matemática
Una sinusoide genérica v(t) se puede definir mediante su frecuencia angular ωi, amplitud A, y fase en el origen de tiempos ϕ. (Notar que ωi, A, y ϕ, son invariantes temporales). Su notación real es:
\begin{equation} v(t) = A\cos(\omega_i t+\phi) \end{equation}
Aplicando los fundamentos básicos de los números complejos explicados arriba, también se puede representar v(t) mediante las siguientes igualdades:
\begin{equation} V = Ae^{j\phi} = A\phase\phi \end{equation}
\begin{equation} v(t) = \real[Ve^{j\omega_i t}] \end{equation}
Es decir, dada una sinusoide v(t) en una frecuencia angular fija ωi, se puede definir un número complejo V, denominado fasor, que permite recuperar el tono original real sin ambigüedades mediante la aplicación de la ecuación (21). Se observa que la señal real se obtiene simplemente mediante la proyección del fasor en movimiento en el eje real.
Obviamente, y aquí radica el potencial de los números complejos en esta aplicación, resulta mucho más sencillo operar con el fasor V que con el tono real v(t). Como veremos en el resto del texto, las operaciones con fasores se pueden simplificar y generalizar para tonos y señales en el interior de un sistema. Y únicamente al final del proceso obtener el tono o señal real de salida de forma simple.
2.1.2 Representación Gráfica
Un fasor se puede ilustrar de dos formas: estática y dinámica, como se ilustra en la siguiente gráfica generada con MATLAB [7]:

La representación estática muestra un vector cuyos módulo y ángulo están determinados por la amplitud A y la fase ϕ de la sinusoide original en el origen de tiempos. En la representación dinámica, el fasor se hace girar a su frecuencia angular añadiendo una fase ωit. Nuevamente, la señal real se obtiene como la proyección del fasor rotatorio en el eje real.
Es inmediato entender que los conceptos ilustrados en este apartado se pueden extender de forma lineal a la operación con un mayor número de fasores independientes. Debido a la dimensión vectorial del plano complejo, se puede operar con fasores del mismo modo que se opera con vectores. Por lo tanto, la suma y resta de fasores de la misma frecuencia da lugar a un fasor que representa de forma unívoca a la señal resultante.
2.2 Dominio de la Frecuencia
Los números complejos facilitan el análisis de sistemas lineales en el dominio de la frecuencia. Por ejemplo, una aplicación clásica de los números complejos en electrónica es la teoría de circuitos [2] en régimen permanente sinusoidal. En práctica, el objetivo de este texto no es repasar los conceptos básicos de teoría de circuitos. Por ello, simplemente se mostrarán matemáticas genéricas en torno a las operaciones asociadas.
Se denota la entrada sinusoidal de un circuito vi(t) mediante su fasor asociado Vi tal que:
\begin{equation} v_i(t) = A_i\cos(\omega_i t+\phi_i) \end{equation}
\begin{equation} V_i = A_ie^{j\phi_i} \end{equation}
La operación del circuito viene determinada por unos elementos lineales: resistencias, condensadores y bobinas. Para el nodo del circuito que representa la salida, se puede obtener una función de transferencia compleja H(ω) respecto al nodo de entrada tal que:
\begin{equation} H(\omega)=|H(\omega)|e^{j\arg{(H(\omega))}}\end{equation}
De forma que el fasor de salida Vo en la frecuencia de trabajo ωi, se obtiene de la siguiente manera:
\begin{equation} V_o =V_i H(\omega)\Bigr|_{\omega=\omega_i}= A_i|H(\omega_i)|e^{j[\phi_i+\arg{(H(\omega_i))}]}\end{equation}
Y, de nuevo, está relacionado unívocamente con la señal real de salida vo(t) mediante la ecuación (21), tal que:
\begin{equation} v_o(t) = A_i|H(\omega_i)|\cos[\omega_i t+\phi_i+\arg{(H(\omega_i))}] \end{equation}
De este modo los fasores permiten simplificar la operación con sinusoides en la resolución de circuitos [2] o sistemas lineales. En general, extendiendo el análisis a todas las frecuencias que componen una señal de entrada, se puede extrapolar la señal de salida del sistema. Otra alternativa es procesar directamente en el dominio del tiempo como se explica a continuación.
2.3 Dominio del Tiempo
En el ejemplo anterior se ha mostrado lo que pasa con un tono en un circuito [2]. Pero el análisis con números complejos se puede generalizar a cualquier sistema lineal, y a todas las frecuencias del sistema analizando directamente las señales en el dominio del tiempo. Para una correcta comprensión de este concepto es necesario estudiar la Transformada de Hilbert [8], y dos formas de señales complejas asociadas a una señal real: la Señal Analítica y la Envolvente Compleja.
2.3.1 Generalización Temporal del Fasor
Un ejemplo práctico, que permite visualizar la utilidad de los números complejos en el procesado lineal de señal, consiste en analizar una constelación de datos tal y como se utiliza en teoría de comunicaciones [6]. Dada una señal en fase i(t) y una en cudratura q(t), formando ambas una constelación paso banda [6] tal que:
\begin{equation} s(t) = i(t)\cos{\left(\omega_c t \right)} + q(t)\sin{\left(\omega_c t \right)} \end{equation}
La señal analítica y la envolvente compleja son, respectivamente:
\begin{equation} s_{a}(t) = [i(t) - jq(t)]e^{j\omega_c t} \end{equation}
\begin{equation} s_{a\downarrow}(t) = [i(t) - jq(t)] \end{equation}
Además, se cumple que:
\begin{equation} s(t) = \real[s_{a}(t)] = \real[s_{a\downarrow}(t)e^{j\omega_c t}] \end{equation}
Comparando la ecuación (30) con las ecuaciones (20) y (21) se observa que la envolvente compleja representa un fasor que cambia a lo largo del tiempo. Se confirma así que las señales analíticas permiten generalizar el análisis complejo más allá de los fasores, extendiéndolo a cualquier señal temporal.
2.3.2 Ejemplo Gráfico
A continuación se ilustra una constelación consistente con la ecuación (27) generada con MATLAB [7]:

Cada símbolo se representa en el plano complejo de forma dinámica con el tiempo. Mientras que la proyección en el eje real de la señal analítica representa la señal real, el módulo del número complejo representa la envolvente de la señal, variante en función del símbolo.
Se observa que la envolvente compleja es equivalente a la representación estática del fasor, aunque variante en el tiempo. Asimismo, la señal analítica reproduce la representación dinámica de cada fasor.
3. Conclusiones de los Números Complejos
Las conclusiones de este texto son las siguientes:
- Los números complejos extienden los números reales añadiendo una parte imaginaria ortogonal a la parte real.
- El operador j, que acompaña a la parte imaginaria, es un elemento matemático cuya esencia es difícil de entender. Sin embargo, gracias a la fórmula de Euler, se puede deducir que el operador j implica un desfase de 90º en sentido contrario a las agujas del reloj.
- Los números complejos permiten simplificar los cálculos y la comprensión de sistemas lineales, como en el caso de teoría de circuitos [2], procesado de señal [3][4] o comunicaciones [5][6].
- La simplificación mencionada en el punto anterior se puede obtener tanto en el dominio del tiempo como en el dominio de la frecuencia.
Bibliografía (Patrocinado)
[1] Electrónica, Allan R. Hambley.
[2] Circuitos Eléctricos, James Nilsson.
[3] Communication Systems, A. Bruce Carlson.
[4] Signals and Systems, A. V. Openheim.
[5] Understanding Digital Signal Processing, Richard Lyons.
[6] Digital Communications, Bernard Sklar.
[7] Guía de MATLAB
[8] Hilbert Transform in Signal Processing, Stephan Hahn.
Suscripción
Si te ha gustado esta contribución no dudes en suscribirte a nuestro boletín:
