La envolvente de una señal paso banda representa a la señal, típicamente banda base, que ejerció como moduladora de la frecuencia portadora. Aunque la potencia de la señal resultante puede variar con el tiempo, su valor se puede generalizar en función de la amplitud de la envolvente.
El siguiente texto muestra la evolución desde el cálculo de la potencia de una sinusoide, hasta el cálculo de la potencia de una señal genérica paso banda en función de la envolvente.
El índice de contenidos es el siguiente:
1. Señales de Potencia Periódicas
Este texto se centra en el contexto de señales paso banda de potencia [1]. Las señales de potencia se extienden en el tiempo proporcionando energía de forma permanente, pero con un valor de potencia limitado.
Dada una señal de potencia periódica s(t) con período T, la potencia promedio P se define como el valor cuadrático medio a lo largo de un período:
\begin{equation} P = \cfrac{1}{T} \int_0^T s^2(t)dt \end{equation}
Notar que se puede establecer una analogía entre la potencia anterior P de una señal teórica y la potencia obtenida en un circuito electrónico. De acuerdo a Teoría de Circuitos [2], la potencia PR generada por una tensión v(t) igual a s(t), y su correspondiente corriente i(t) en una resistencia R, es igual a:
\begin{equation} P_R= \cfrac{1}{T} \int_0^T v(t)i(t)dt = \cfrac{1}{RT} \int_0^T v^2(t)dt = \cfrac{P}{R} \end{equation}
En resumen, ambas potencias son iguales para una resistencia normalizada R=1.
2. Envolvente de una Señal
La siguiente gráfica, tomada de nuestra explicación de la velocidad de grupo, muestra diversos ejemplos simples de señales paso banda y sus correspondientes envolventes.

La gráfica muestras señales a lo largo del espacio en un instante de tiempo. Para el resto del texto, se considerarán de forma equivalente y sin perder generalidad señales temporales en un punto del espacio.
2.1 Envolvente Sinusoidal Constante
A continuación se considera el caso más simple, una sinusoide de amplitud A y envolvente constantes:
\begin{equation} s(t) = A\cos(\omega t) \end{equation}
La representación gráfica se corresponde con el caso (c) de la imagen anterior.
Aplicando la ecuación (1), y tras varias manipulaciones trigonométricas simples, se obtiene un valor de potencia constante:
\begin{equation} \begin{split} P &= \cfrac{1}{T} \int_0^T s^2(t)dt \\ &= \cfrac{A^2}{T} \int_0^T \cos^2(\omega t)dt \\ &= \cfrac{A^2}{2T} \int_0^T [1+\cos(2\omega t)]dt \\ &= \cfrac{A^2}{2} \end{split}\end{equation}
El último paso se produce porque la integral de una sinusoide a lo largo de un número entero de períodos es igual a cero.
A continuación se demuestra que este resultado se puede extrapolar a la potencia de una señal paso banda con envolvente genérica.
2.2 Envolvente Genérica
2.2.1 Cálculo de la Potencia
Cualquier señal paso banda s(t) se puede escribir en función de sus componentes en fase, i(t), y cuadratura, q(t) [1]. Matemáticamente:
\begin{equation} s(t) = i(t)\cos{\left(\omega_c t \right)} + q(t)\sin{\left(\omega_c t \right)} \end{equation}
Debido a la evolución de las amplitudes de i(t) y q(t), la potencia de la señal puede variar en el tiempo. Aplicando la ecuación (1), y teniendo en cuenta que el periodo T de la portadora sí es constante, se obtiene que:
\begin{equation} \begin{split} P(t) &= \cfrac{1}{T} \int_t^{t+T} s^2(t)dt \\ &= \cfrac{1}{T} \int_t^{t+T} [i^2(t)\cos^2(\omega t) + q^2(t)\sin^2(\omega t) + 2i(t)q(t)\cos(\omega_c t)\sin(\omega_c t)]dt \end{split}\end{equation}
Para avanzar en los cálculos se debe realizar el siguiente razonamiento. Primero, tanto i(t) como q(t) son señales banda base. Segundo, si la frecuencia de la portadora es suficientemente alta, i(t) y q(t) se pueden considerar constantes a lo largo de un periodo T. En consecuencia, la ecuación (6) se puede resolver de la siguiente manera:
- Por analogía con (4), la primera integral será igual al cuadrado de i(t) dividido por dos.
- Por analogía con el punto anterior, la segunda integral será igual al cuadrado de q(t) dividido por dos.
- Aplicando trigonometría básica, la tercera integral es equivalente a la integral de una sinusoide con frecuencia doble a la portadora. Y, nuevamente por analogía con (4), será igual a cero.
En resumen, se obtiene que:
\begin{equation}P = \cfrac{i^2(t) + q^2(t)}{2} \end{equation}
2.2.2 Relación entre Potencia y Envolvente
A partir del análisis de la señal analítica y la envolvente compleja de s(t), se demuestra que su envolvente e(t) es igual a:
\begin{equation} e(t) = |s_{a\downarrow}(t)| = \sqrt{i^2(t) + q^2(t)} \end{equation}
Por lo tanto, a partir de (7) y (8), se deduce que:
\begin{equation} P = \cfrac{e^2(t)}{2} \end{equation}
Así se obtiene la analogía entre las ecuaciones (4) y (9). Dada una señal paso banda, la envolvente instantánea viene dada por el módulo de la señal en el plano complejo:
- En el caso de una sinusoide, esta envolvente es siempre constante, como se observa en la siguiente gráfica:
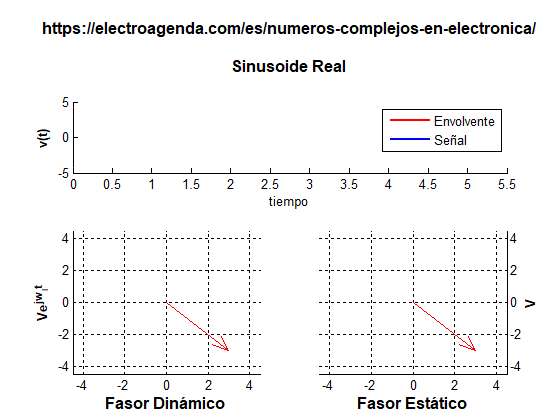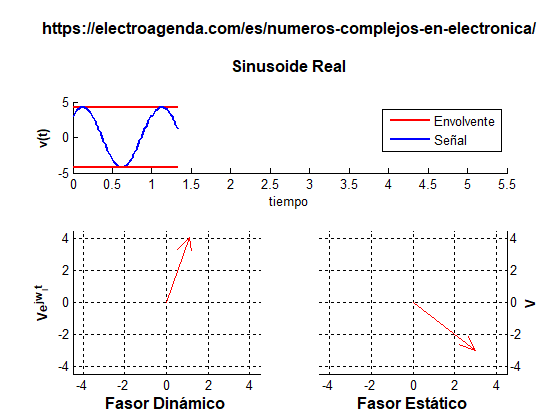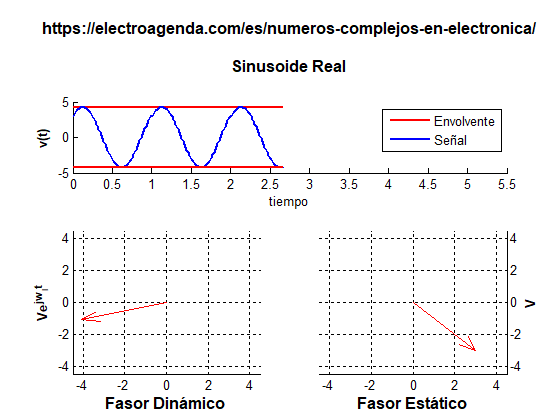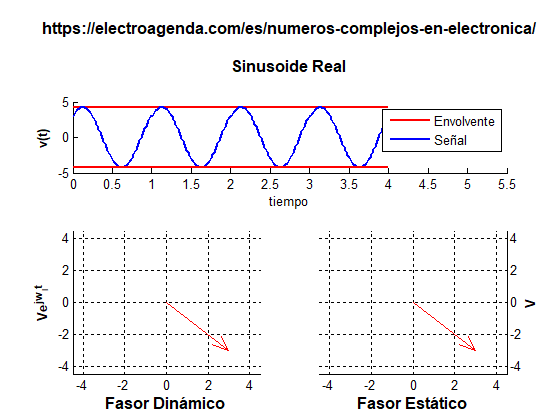
- En una señal con componentes en fase y cuadratura, la envolvente instantánea es una consecuencia de ambas componentes, como se refleja en el siguiente ejemplo (por simplicidad, la frecuencia central se ha reducido y las transiciones entre símbolos se han eliminado):

Una vez determinada la envolvente, en todos los casos la potencia instantánea se obtiene con la ecuación (9).
3. Conclusiones
El texto se puede resumir en los siguientes conceptos:
- La potencia de una señal paso banda evoluciona de forma directamente proporcional a su envolvente.
- La envolvente de una sinusoide simple es su amplitud.
- La envolvente de una señal paso banda más compleja se obtiene directamente a partir de sus componentes en fase y cuadratura.
- El plano complejo permite visualizar simultáneamente las componentes en fase y cuadratura junto con la envolvente instantánea de la señal.
Bibliografía (Patrocinado)
[1] Communication Systems, A. Bruce Carlson.
[2] Circuitos Eléctricos, James Nilsson.
Suscripción
Si te ha gustado esta contribución no dudes en suscribirte a nuestro boletín:
