La envolvente compleja es una señal analítica banda base. Se obtiene suprimiendo las frecuencias negativas (o positivas) de una señal real paso banda, y trasladando el contenido espectral restante a banda base. Debido a la notación compleja y a la eficiencia espectral de la señal resultante, la envolvente compleja es muy útil tanto en la simulación de sistemas lineales como en el procesado de señal digital en tiempo real.
Los conceptos anteriores son explicados en profundidad en este texto, enfocándose principalmente en la implementación de la envolvente compleja. El texto está organizado con el siguiente índice:
1. Definición de la Envolvente Compleja
En este apartado se describe la representación espectral y las matemáticas fundamentales de una señal real paso banda y su correspondiente envolvente compleja. Para una correcta comprensión del texto se recomienda repasar los siguientes enlaces sobre La Transformada de Hilbert y sobre La Señal Analítica.
1.1 Representación Espectral
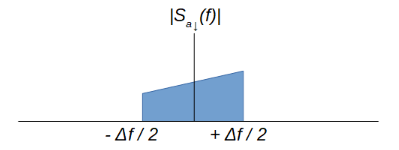
En la siguiente imagen se ilustra el espectro de una señal real paso banda y su envolvente compleja correspondiente:

Espectralmente, la envolvente compleja se obtiene trasladando las frecuencias positivas a banda base, y suprimiendo el contenido espectral negativo original. Mientras que la señal original es real y, por tanto, hermítica, la señal resultante no cumple los principios de la hermiticidad, confirmando que se trata de una señal compleja.
Gráficamente se observa que el ancho de banda de la envolvente compleja es la mitad que el de la señal original. Por lo tanto, de acuerdo al criterio de Nyquist, la envolvente compleja se puede muestrear a la mitad de velocidad que la señal paso banda.
Finalmente, indicar que este texto muestra la envolvente compleja obtenida a partir de las frecuencias positivas. Sin embargo, es posible realizar el procesado equivalente con las componentes frecuenciales negativas, como se muestra en el siguiente enlace.
1.2 Demostración Matemática
En este apartado se muestra el procesamiento matemático para obtener la envolvente compleja a partir de la señal paso banda real. Asimismo, se analiza el procedimiento complementario que obtiene una señal paso banda real a partir de su envolvente compleja asociada. También se desarrolla el caso en que la señal paso banda real se define en términos de sus componentes en fase y cuadratura, muy útil para el análisis matemático de señales de comunicaciones.
1.2.1 Señal Genérica
Sea s(t) una señal real paso banda genérica. Su Transformada de Hilbert viene dada por \footnotesize \hat{s}(t) [1]. La señal analítica sa(t), en la que se han suprimido las frecuencias negativas, se obtiene así:
\begin{equation} s_{a}(t) = s(t)+j\hat{s}(t) \end{equation}
La demostración de que el espectro de la señal analítica, Sa(f), no contiene el contenido espectral negativo de s(t) es casi inmediata:
\begin{equation} S_a(f) = \begin{cases}S(f)+j[-jS(f)] =2S(f)&\text{for } f >0 \\ S(f)+j0 =S(f)&\text{for } f =0 \\ S(f)+j[jS(f)]=0 &\text{for } f<0 \end{cases} \end{equation}
A partir de la señal analítica, el equivalente banda base se obtiene trasladando las frecuencias positivas restantes a banda base. Para no generar otras réplicas, es necesario multiplicar la señal analítica por el fasor localizado en la frecuencia central o portadora [2]. De esta forma, la envolvente compleja se obtiene así:
\begin{equation} s_{a\downarrow}(t) = s_{a}(t)e^{-j\omega_c t} \end{equation}
Finalmente, dada una envolvente compleja, su señal real paso banda asociada se obtiene realizando el proceso inverso que se desprende de las ecuaciones (1) y (3):
\begin{equation} s(t) = \real[s_{a}(t)] = \real[s_{a\downarrow}(t)e^{j\omega_c t}] \end{equation}
1.2.2 Señal en Fase y Cuadratura
Resulta de especial interés matemático y conceptual desarrollar el procedimiento matemático anterior partiendo de una señal genérica s(t) expresada en función de sus componentes en fase, i(t), y cuadratura, q(t). Es decir:
\begin{equation} s(t) = i(t)\cos{\left(\omega_c t \right)} + q(t)\sin{\left(\omega_c t \right)} \end{equation}
Aplicando (1) y (3) en (5), como se demuestra en este enlace, se obtiene la envolvente compleja asociada:
\begin{equation} s_{a\downarrow}(t) = [i(t) - jq(t)] \end{equation}
Por lo tanto, cualquier implementación de la envolvente compleja a partir de s(t) debe dar lugar al resultado obtenido en (6).
2. Implementación de la Envolvente Compleja
La envolvente compleja es muy útil en el procesado de señal y de sistemas típicamente lineales [2][3], como se muestra en este enlace. Debido a la naturaleza compleja de la señal, su implementación electrónica [4][5][6] siempre lleva asociada una parte estrictamente digital. Aunque la entrada y/o salida del sistema global pueda ser analógica.
La implementación de la envolvente compleja se puede realizar a diversos niveles, cubriendo parcial o totalmente un sistema. Por ejemplo, la envolvente compleja se podría utilizar para las siguientes funciones:
- Procesado de una señal entrante, como en el demodulador de un receptor.
- Generación de una señal saliente, como en el modulador de un transmisor.
- Regeneración y/o modificación de una señal: implica la combinación de los dos puntos anteriores.
En este apartado se analiza la implementación de la envolvente compleja tanto a nivel puramente analítico y de simulación, como para sistemas en tiempo real.
2.1 Procesado en Tiempo Simulado
La implementación de la envolvente compleja para simular un sistema se deriva directamente de las ecuaciones mostradas en el apartado 1.2. Las señales generadas como fuente de la simulación deben seguir la estructura de la ecuación (6), en su versión digital:
\begin{equation} s_{a\downarrow}(n) = s_{a\downarrow}(n't_s) = [i(n't_s) - jq(n't_s)] = [i(n) - jq(n)] \end{equation}
Donde n’ y ts representan el número de muestra y el tiempo de muestreo respectivamente. Por simplicidad, en el resto del texto se empleará la variable n, que es igual al producto de n’ y ts. Aunque en la práctica n=t, por claridad se empleará la t como variable independiente en señales analógicas, y la n en el caso de señales discretas.
Todos los elementos del sistema simulado, ya sean banda base o paso banda, deben implementarse con su envolvente compleja digital asociada a la frecuencia central del elemento en particular. Por ejemplo, la función de transferencia de un filtro real paso banda debe trasladarse en frecuencia para obtener su envolvente compleja.
De este modo, la simulación del sistema permite obtener la señal en cualquier parte de la cadena. La obtención de la señal paso banda real asociada a cada envolvente compleja se obtendría con la ecuación (4) en su versión digital:
\begin{equation} s(n) = \real[s_{a\downarrow}(n)e^{j\omega_c n}] \end{equation}
Este es el método de simulación empleado en simuladores de sistemas como SystemVue, QucsStudio o MATLAB/Octave [7]. Por ejemplo, con este último se realizó la siguiente simulación, que genera una modulación digital en cuadratura y donde la duración de cada símbolo coincide con un período de la portadora:

2.2 Procesado en Tiempo Real
En sistemas en tiempo real, una vez que se dispone de la envolvente compleja, todas las ideas explicadas en el apartado 2.1 aplican por igual. Además, en este caso es necesario garantizar que todas las operaciones matemáticas digitales, como filtrados, deben cumplir con la temporización asociada a la frecuencia de muestreo de la señal. Por lo tanto, la tecnología seleccionada para el procesado (ASIC, uC o FPGA) debe ser capaz de soportar la velocidad de operación necesaria.
Una dificultad esencial de los sistemas en tiempo real es el paso desde la señal paso banda, típicamente analógica, a la envolvente compleja y viceversa. En esta sección se muestran diversos esquemas para realizar ese proceso, y se clasifican en función del número de conversores analógico-digital -ADC- (o digital-analógico -DAC-) que se emplean en la implementación .
2.2.1 Señal Paso Banda => Envolvente Compleja
A continuación se describe cómo obtener la envolvente compleja a partir de la señal real paso banda usando uno o dos ADC. En todos los casos se enumeran las ventajas y desventajas de cada implementación.
2.2.1.1 Implementación con 1 ADC
El siguiente esquema permite obtener la envolvente compleja a partir de la señal real paso banda usando un ADC:

En primer lugar es necesario muestrear directamente la señal paso banda. Entonces, una vez digitalizada la señal, se debe mezclar con un fasor centrado en la frecuencia de la portadora para trasladarse a banda base. Finalmente, un último filtro paso bajo (LPF) elimina las réplicas no deseadas.
Notar que, por simplicidad, en la imagen de arriba el muestreado se realiza en la primera zona de Nyquist. Pero también es posible muestrear en otras zonas de Nyquist, de forma que la frecuencia central de la señal digitalizada podría no coincidir con la de la señal analógica.
La señal compleja se obtiene justo después de la multiplicación por el fasor para la traslación en frecuencia. Hasta ese momento, la parte imaginaria de la señal digital es igual a cero. En la práctica, esta traslación puede implementarse usando varias estrategias:
- Si no se dispone de multiplicadores en el dispositivo digital físico, se pueden emplear algoritmos como el CORDIC.
- Si la tecnología empleada dispone de multiplicadores lo suficientemente rápidos, se puede emplear un NCO y un mecanismo que obtenga las muestras del seno y coseno necesarias para general el fasor. Típicamente se emplearían memorias para almacenar muestras fijas del seno/coseno, y potencialmente interpoladores para calcular muestras intermedias e incrementar la precisión.
La principal ventaja de esta implementación es que solo requiere un conversor ADC. Sin embargo, la desventaja asociada es que la frecuencia de muestreo del ADC debe ser al menos el doble de la requerida por la envolvente compleja. Esto se debe a que se muestrea directamente la señal paso banda en lugar de una señal banda base.
2.2.1.2 Implementación con 2 ADC
Mediante la conversión de la señal real paso banda a banda base en un primer paso, se consigue minimizar la frecuencia de muestreo necesaria. En consecuencia, se podría reducir la potencia asociada a la conversión. Sin embargo, este esquema presenta la desventaja de requerir 2 ADCs, como se muestra en la siguiente imagen:

A continuación se proporciona la justificación matemática de esta implementación. Sea s(t) la señal definida en la ecuación (5). Tras multiplicar por las sinusoides en fase y en cuadratura respectivamente, se obtiene que:
\begin{equation} s_i(t) = 2i(t)\cos^2{\left(\omega_c t \right)} + 2q(t)\sin{\left(\omega_c t \right)}\cos{\left(\omega_c t \right)} \end{equation}
\begin{equation} s_q(t) = 2i(t)\cos{\left(\omega_c t \right)}\sin{\left(\omega_c t \right)} + 2q(t)\sin^2{\left(\omega_c t \right)} \end{equation}
Tras aplicar las siguientes igualdades trigonométricas:
\begin{equation} \cos^2{\left(\omega_c t \right)} = \cfrac{1}{2} +\cfrac{\cos{\left(2\omega_c t \right)}}{2} \end{equation}
\begin{equation} \sin{\left(\omega_c t \right)}\cos{\left(\omega_c t \right)} = \cfrac{\sin{\left(2\omega_c t \right)}}{2} \end{equation}
\begin{equation} \sin^2{\left(\omega_c t \right)} = \cfrac{1}{2} -\cfrac{\cos{\left(2\omega_c t \right)}}{2} \end{equation}
Se obtiene que:
\begin{equation} s_i(t) = i(t) + i(t)\cos{\left(2\omega_c t \right)} + q(t)\sin{\left(2\omega_c t \right)} \end{equation}
\begin{equation} s_q(t) = i(t)\sin{\left(2\omega_c t \right)} + q(t) - q(t)\cos{\left(2\omega_c t \right)} \end{equation}
Si las componentes en fase y cuadratura, i(t) y q(t), están limitadas en banda, y la frecuencia de la portadora es lo suficientemente alta, a la salida de los filtros paso bajo (LPF) se obtiene que:
\begin{equation} s_i(t) \xRightarrow{LPF} i(t) \end{equation}
\begin{equation} s_q(t) \xRightarrow{LPF} q(t) \end{equation}
Por lo tanto, se habrían recuperado las componentes en fase y cuadratura originales. Finalmente, la secuencia que se procesa de forma discreta es [i(n)–jq(n)] como se mostró en la ecuación (7).
Notar que esta demostración se apoya en los cálculos presentados en el apartado 1.2.2 para llegar a la ecuación (6). Pero también es posible realizar una demostración exclusivamente gráfica partiendo del espectro paso banda original [8].
2.2.2 Envolvente Compleja => Señal Paso Banda
La transición desde la envolvente compleja a su señal paso banda real asociada se puede realizar con esquemas complementarios a los expuestos en el apartado anterior.
2.2.2.1 Implementación con 1 DAC
La implementación con 1 DAC se realiza con el siguiente esquema:
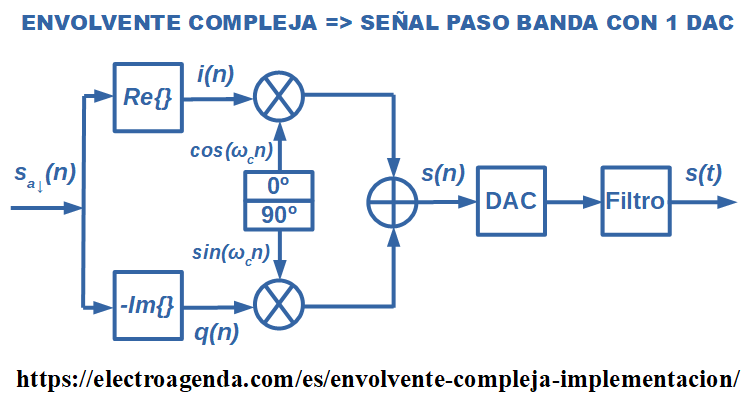
A partir de la envolvente compleja se pueden separar las componentes en fase y cuadratura. Estas últimas se suben en frecuencia de forma completamente digital, con técnicas equivalentes a las explicadas en la sección 2.2.1.1. Finalmente, un DAC más un filtro que elimine réplicas no deseadas permite recuperar la señal real paso banda asociada.
De forma equivalente, la ventaja de esta estrategia radica en que sólo es necesario un conversor. Sin embargo, la principal desventaja es que la frecuencia de muestreo de trabajo no es óptima, puesto que se opera con señales paso banda en el dominio discreto.
2.2.2.2 Implementación con 2 DAC
La implementación con 2 DAC se realiza con el siguiente esquema:

En este caso, a partir de la envolvente compleja se generan las componentes en fase y cuadratura banda base. Entonces, empleando dos DACs, se obtienen las correspondientes señales temporales. Finalmente, la conversión a alta frecuencia se realiza en el dominio analógico.
Las ventajas y desventajas son las correspondientes al esquema equivalente descrito en la sección 2.2.1.2. La frecuencia de muestreo con la que se trabaja en el domino discreto es la más baja posible, al operar con señales banda base. Como contrapartida, es necesario utilizar dos DACs.
3. Conclusiones de la Envolvente Compleja
Las principales conclusiones del texto sobre la envolvente compleja son las siguientes:
- La envolvente compleja es una señal analítica banda base asociada a una señal real paso banda.
- Se obtiene suprimiendo las frecuencias negativas de la señal original y trasladando las frecuencias positivas a banda base.
- Las principales ventajas de la envolvente compleja son las asociadas a la notación compleja (separación de componentes en fase y cuadratura; y facilidad para obtener amplitud y fase instantáneas de la señal) y la eficiencia espectral (procesado del espectro de interés sin solapes ni componentes frecuenciales duplicadas).
- Es muy útil en el procesado de señales y sistemas, tanto simulados como en implementaciones de tiempo real.
- En sistemas de tiempo real, la envolvente compleja se puede obtener a partir de la señal paso banda usando 1 o 2 ADCs. De forma equivalente, el paso de una envolvente compleja a la señal real paso banda asociada se puede realizar con 1 o 2 DACs.
- Las implementaciones con 1 conversor tienen la desventaja de emplear una frecuencia de muestreo de al menos dos veces la mínima teórica, que es la obtenida en implementaciones con 2 conversores.
- Las implementaciones con 2 conversores emplean más recursos, pero minimizan la frecuencia de muestreo y, potencialmente, la potencia de la conversión.
Bibliografía
[1] Hilbert Transform in Signal Processing, Stephan Hahn.
[2] Communication Systems, A. Bruce Carlson.
[3] Signals and Systems, A. V. Openheim.
[4] Circuitos Eléctricos, James Nilsson.
[5] Electrónica, Allan R. Hambley.
[6] Electronic Principles, A. Malvino.
[7] Guía de MATLAB
[8] Understanding Digital Signal Processing, Richard Lyons.
[9] Cursos de Procesado de Señal
Suscripción
Si te ha gustado esta contribución no dudes en suscribirte a nuestro boletín: