The term laser is used as a noun, but it was originally an acronym for “light amplification by stimulated emission of radiation”. A laser is a fundamental part in any optical transmitter, as it is the generator of the optical carrier. In optical communications, the spectral location of a carrier is often stated in wavelengths (typically nm) instead of frequencies.
This article reviews the fundamental concepts of lasers employed in optical communications, with the following table of contents:
1. Physics of the Laser
This section briefly describes the physical principles that explain the operation of optical sources [1]. The energy of an electron depends on the position of its orbit with respect to the nucleus. Higher energies are required for orbits farther from the nucleus.
1.1 Absorption
If the electron is in an inner orbit with a low energy E1, it can absorb the energy from a source of light (photon) and move to the orbit with higher energy E2. This process, called absorption, is illustrated in Figure 1(a). The energy provided by the photon is equal to ΔE=E2–E1=hν, where h is the Planck´s constant and ν is the frequency of the incident light.
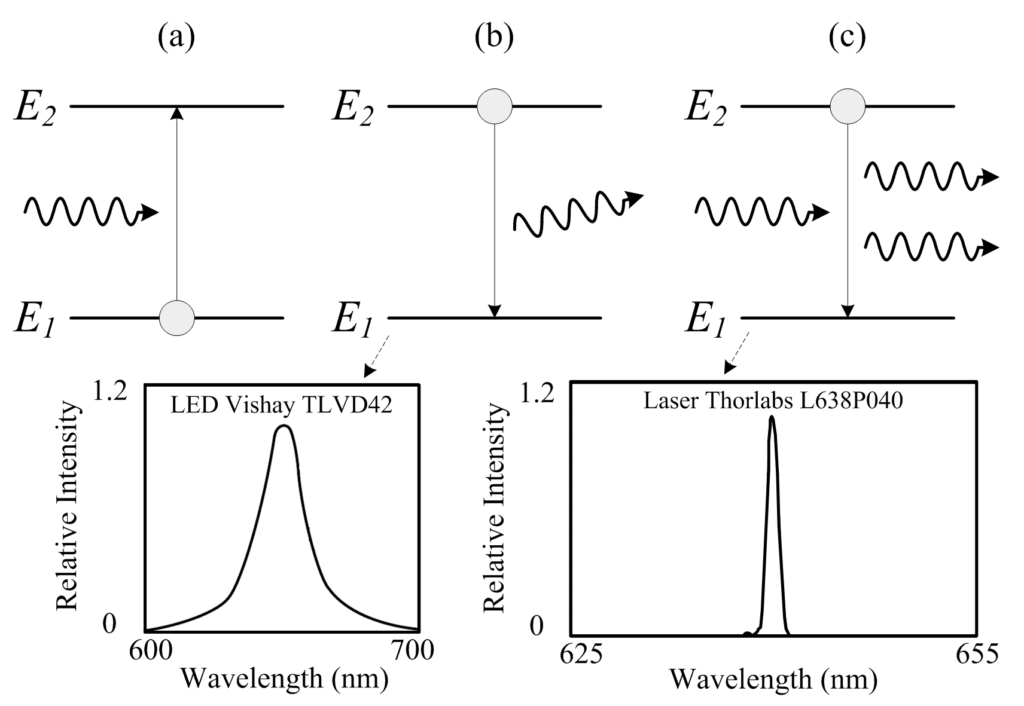
1.2 Spontaneous Emission
The opposite process, called emission, also occurs. An electron in an external orbit E2 tends to return to the internal orbit E1 emitting a photon with energy ΔE, as it can be seen in Figure 1(b). When this phenomenon occurs randomly it is called spontaneous emission.
If multiple photons are generated in this way, they present different and random phases and directions producing incoherent light, as in a Light Emitting Diode (LED). Although all the photons have the same frequency, the sum of multiple tones with arbitrary phases translates into a random modulation that significantly spread the spectrum. As a consequence, the performance of LEDs in communications is greatly limited. An example of a commercial LED spectrum is also shown in Figure 1(b).
1.3 Stimulated Emission
In contrast, lasers are based on stimulated emission. If one electron occupies the excited level E2 and one photon with energy ΔE enters in the atom, the electron will come back to the level E1 but releasing a new photon that is in phase and has the same direction as the incident one, as illustrated in Figure 1(c). When multiple photons are generated in this way, a coherent source of light with a narrow spectral range is produced, as it is also shown in Figure 1(c) for a commercial device.
A laser is formed of a material whose electrons are continuously excited, by an outside source of light or by an electric field, to occupy higher energy levels in a process known as population inversion. A structure based on mirrors with different reflectivity ensures that multiple photons are travelling repeatedly through the medium, generating more stimulated coherent photons in a chain reaction [1].
1.4 Laser Relative Intensity Noise and Phase Noise
Light is an electromagnetic field and lasers are the sources of carriers at optical frequencies. The lasers employed in communications are typically based on semiconductors. Similarly to an electrical oscillator, the spectrum of a laser is not a perfect delta corresponding to a pure tone.
As undesired spontaneous emission also occurs inside a laser, random small fields with arbitrary phases are continuously added to the coherent tone. This effect perturbs the amplitude and the phase of the output generating Relative Intensity Noise (RIN) [1] and phase noise respectively. RIN is usually measured in dBc/Hz and phase noise in terms of spectral linewidth (Hz). Obviously, both effects can have an impact on the performance of optical communication systems.
2. Direct Modulation of a Laser
2.1 Fundamentals
Semiconductor lasers can be seen as laser diodes whose output amplitude and power depends on the driving current. Neglecting RIN and phase noise, the electric field at the output of a monochromatic laser can be written as:
\begin{equation} E(t) = E_p(t)\cos(\omega_ct) \end{equation}
where Ep(t) is the peak amplitude and ωc is the frequency of the optical carrier.
The term Ep(t) is a function of time reflecting the fact that the amplitude depends on the current that drives the laser diode. Note that Ep(t) can only vary at the rate of an electrical signal and, as a consequence, the frequency of change is several orders of magnitude lower than the optical frequency ωc. Thus, at the output of the laser, the average power P (also called intensity) with respect to the optical frequencies is:
\begin{equation} P(t) = \langle E^2(t) \rangle = \langle E^2_p(t)\cos^2(\omega_ct) \rangle = \cfrac{E^2_p(t)}{2} \end{equation}
It can be readily seen that an optical communication link can be established by modulating the power or intensity of the carrier with the information to be transmitted. From the point of view of the signal this process is called Intensity Modulation (IM). From the point of view of the device it is also called direct modulation, in contrast with external modulation which is performed with additional devices.
2.2 Transfer Function of the Laser
As illustrated in Figure 2, the transfer function of a laser diode presents an approximately linear area in which the output power P is proportional to the driving current i(t). This area begins for a current above a given threshold ith, so that the laser must be biased with a higher current ib that produces a DC power Pb to ensure linear operation.
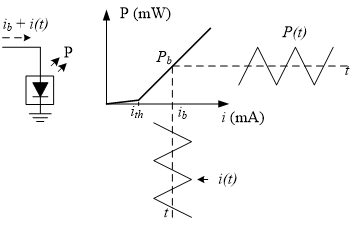
Mathematically, assuming a proportionality factor m:
\begin{equation} P(t) = P_b + m·i(t) \end{equation}
\begin{equation} E(t) = \sqrt{2P(t)}\cos(\omega_ct) \end{equation}
2.3 Performance and Limitations
Performance of direct modulation is limited by several concepts:
- Firstly, the RIN degrades the Signal to Noise Ratio (SNR) of the power signal at the output of the laser [1].
- Secondly, different optical powers produce a frequency deviation in the output wavelength in a phenomenon known as chirp. Consequently, directly modulated lasers present a broadening in the output spectrum that translates into impairments in the received signals due to fibre dispersion.
- Thirdly, the bandwidth of the modulation is limited [1] so that broadband lasers are difficult and costly to build.
- Finally, it is not possible to perform direct modulation of the electric field and the phase of the laser. Phase modulation is required for coherent systems and also to produce Optical Single Side Band (OSSB) signals.
While the RIN and linewidth are inherent properties of the laser that cannot be avoided, external modulation can be employed to overcome the rest of the limitations.
3. Classification of Communication Lasers
3.1 Wavelength
Three spectral regions are usually employed in optical communications:
- The first window corresponds to the range of 800-900 nm. The first optical links used these wavelengths because early fibre presented minimum losses in that region. Although the losses in that area are high in current fibre, these wavelengths are still used for short distances due to the low cost of lasers and detectors.
- The second band of interest is around 1310 nm. This band is attractive because there is zero dispersion fibre available, although sources and detectors are more costly.
- Finally, the last band of interest is around 1550 nm as fibre losses are the lowest there. Although fibre dispersion is not zero, it can be compensated electronically or optically to achieve longer transmission distances.
3.3 Structure
According to the internal structure, several types of monochromatic semiconductor lasers are typically employed in communications [1]: Distributed Feedback Lasers (DFB), External Cavity Lasers (ECL), and less costly Vertical Cavity Surface Emitting Lasers (VCSEL). Their typical parameters are shown in Figure 3.

Bibliography (Sponsored)
[1] Fiber-Optic Communication Systems, Govind P. Agrawal
[2] Diode Lasers and Photonic Integrated Circuits, L. Coldren
Subscription
If you liked this contribution, feel free to subscribe to our newsletter:
